[알고리즘] Chapter 3. 동적계획(Dynamic Programming)

경희대학교 한치근 교수님의 알고리즘 수업을 기반으로 정리한 글입니다.

 

Dynamic Programming

• divide-and-conquer(분할정복식, 재귀): top-down 해결법
• Dynamic Programming: bottom-up 해결법
  • 작은 문제 해결 먼저 -> 결과를 큰 문제의 해결로 확산
    1. 재귀 관계식(recursive property) 정립
    2. 작은 사례를 먼저 해결하는 상향식 방법으로 진행

 

1. 이항계수 구하기

• 문제: 이항계수를 계산
• 입력: 음수가 아닌 정수 n과 k, 여기서 k <= n
• 출력: bin, nCk

- 시간복잡도(분할정복식 접근방법)

• 귀납증명에 따라, nCk를 구하기 위해서 알고리즘이 계산하는 항(term)의 개수는 2*nCk - 1

 

- 동적계획법 알고리즘 설계전략

1. recursive property 정립
2. nCk를 구하기 위해서 B[0][0]부터 시작하여 위에서 아래로 재귀 관계식을 적용하여 배열을 채워 나가면 됨

• 총 수행횟수는 ∈ Θ(nk)

 

2. 최단경로 문제(all-pairs shortest paths problem)

- 그래프 용어

• 정점(vertex, node), 이음선(edge, arc)
• 방향 그래프(directed graph/digraph)
• 가중치(weight), 가중치 포함 그래프(weighted graph)
• 경로(path): 각 정점에서 다음 정점을 잇는 이음선이 존재하는 일련의 정점들
• 단순경로(simple path): 같은 정점을 두 번 지나지 않는 경로
• 순환(cycle): 한 정점에서 다시 그 정점으로 돌아오는 경로
• 순환 그래프(cyclic graph) vs 비순환 그래프(acyclic graph)
  • cycle이 있는 그래프 vs 없는 그래프
• 길이(length): 경로상에 있는 가중치의 합(가중치 포함 그래프). 경로상의 이음선의 개수(가중치가 없는 그래프)

2.1. all-pairs shortest paths problem

• 문제: 가중치 포함, 방향성 그래프에서 최단경로 찾기
• 최적화문제(optimization problem)
  
  • 주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 optimal solution을 찾아야 하는 문제

- Adjacency Martix: W

- Brute-force algorithm

• 한 정점에서 다른 정점으로의 가능한 모든 경로들의 길이를 구한 뒤, 그들 중에서 최소 길이의 경로를 탐색
• 분석
  • n개의 정점이 모두 연결된 상태
  • 처음에 선택 가능한 정점 n-2개, n-1개, ...
  • 총 경로의 개수는 (n-2)! -> 지수함수보다 큰 시간복잡도 비효율적!

- Dynamic Programming 

• case 1: { v1, v2, .. ,vk }의 정점들만을 통해서, v_i에서 v_j로 가는 최단경로가 v_k를 거치지 않는 경우
• case 2: { v1, v2, .. ,vk }의 정점들만을 통해서, v_i에서 v_j로 가는 최단경로가 v_k를 거치는 경우

2.2. Floyd의 알고리즘 1

• 문제: 가중치 포함 그래프의 각 정점에서 다른 모든 정점까지의 최단거리를 계산하라
• 입력: 가중치 포함, 방향성 그래프 W와 그 그래프에서의 정점의 수 n
• 출력: 최단거리의 길이 포함된 배열 D

- 시간복잡도

• every case
• 단위연산: for-j 루프 안의 지정문
• 입력크기: 그래프에서의 정점의 수 n
  • T(n) = n * n * n = n^3 ∈ Θ(n^3)

- 3차원 배열이 필요하지 않은 이유

• k는 가장 늦게 증가하기 때문에, k번째 node를 경유하는 상태를 계산할 때, k를 중간에 넣기 전 상태이므로 덮어써도 문제 없음

 

2.3. Floyd의 알고리즘 2

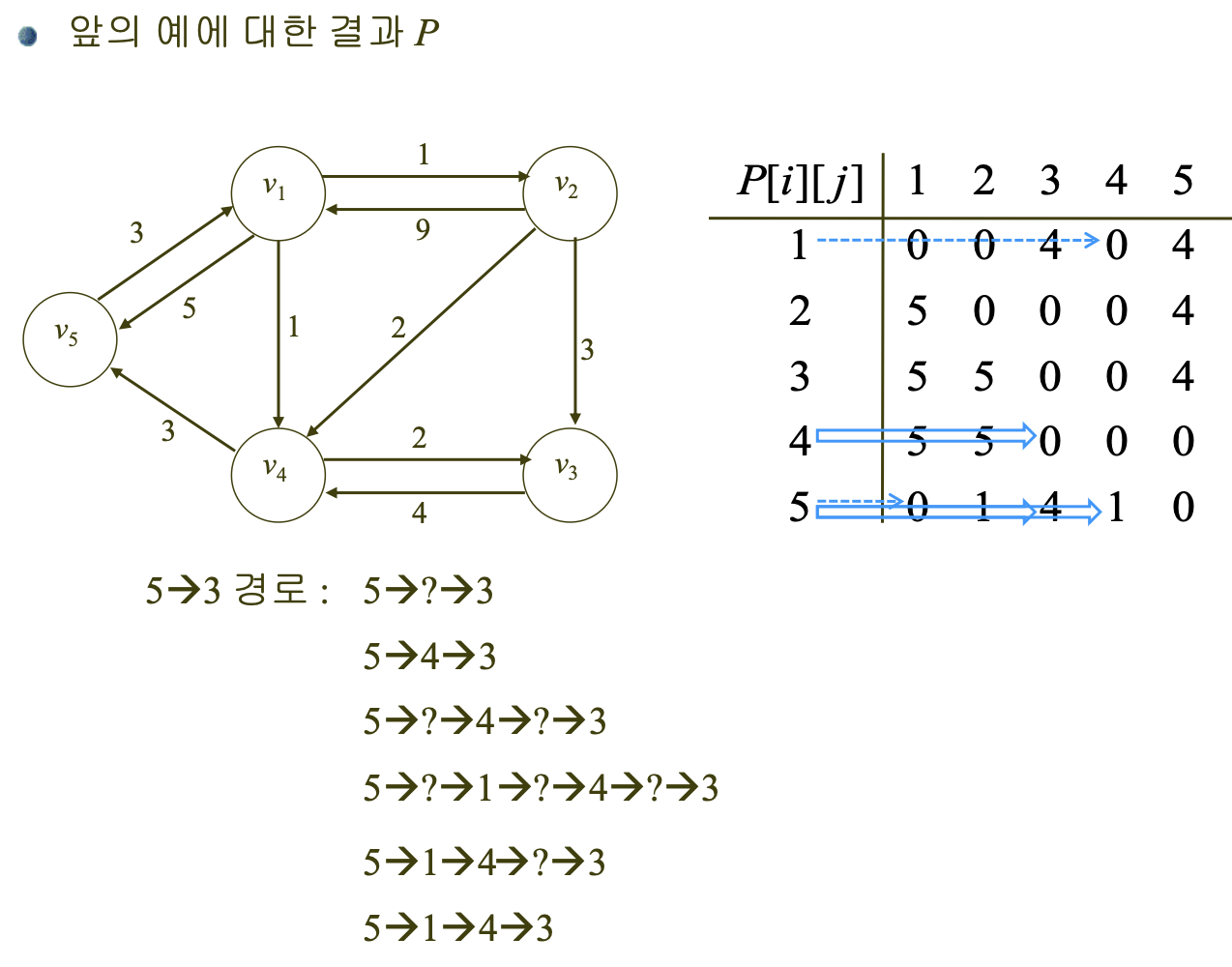
• 출력: 최단경로의 길이가 포함된 배열 D, 다음을 만족하는 배열 P
• P[i][j]: i에서 j까지 가는 최단 경로 중, j 바로 이전에 들른 노드
  • vi에서 vj까지 가는 최단경로의 중간에 놓여 있는 정점이 최소한 하나는 있는 경우 -> 놓여 있는 정점 중에서 가장 큰 인덱스
  • 최단경로의 중간에 놓여 있는 정점이 없는 경우 -> 0

2.4. 최적의 원칙

• the principle of optimality: 어떤 문제 사례에 대한 최적 해가 그 사례를 분할한 부분 사례에 대한 최적해를 항상 포함하고 있는 경우
• 최적의 원칙이 적용되어야 -> 동적 계획법 사용 가능
  • ex) 최단 경로 구하는 문제에서, vk를 vi에서 vj로 가는 최적 경로 상의 정점이라고 하면
  • vi에서 vk로 가는 부분경로 & vk에서 vj로 가는 부분경로도 반드시 최적이어야 함

- 최적의 원칙이 적용되지 않는 예: 최장경로(longest path) 문제

• v1에서 v4로의 최장경로는 [v1, v3, v2, v4]
• 그러나 이 경로의 부분경로인 v1에서 v3으로의 최장경로는 [v1, v3]이 아니고, [v1, v2, v3]이다.

3. 연쇄 행렬 곱셈(matrix-chain multiplication)

• i x j 행렬과 j x k 행렬을 곱하기 위해서는 i x j x k번의 곱셈이 필요
• 연쇄적으로 행렬곱셈을 수행할 때, 어떤 행렬곱셈을 먼저 수행하느냐에 따라 필요한 총 곱셈의 횟수가 달라짐
• ex) A1 x A2 X A3
• A1의 크기는 10 X 100, A2의 크기 100 X 5, A3의 크기 5 X 50
• (A1 X A2) X A3 곱셈의 총 횟수 7500 = 5000 + 2500
  • (10 * 100 * 5) + (10 * 5 * 50)
• A1 X (A2 X A3) 곱셈의 총 횟수 75000 = 25000 + 50000
  •  (10 * 100 * 50) + (100 * 5 * 50)

3.1. Brute-force

• 시간복잡도 최소 exponential-time

• Brute Force의 모든 가능한 가지 수 P(n)
  • P(n) = C(n - 1): Catalan Number

-> n이 커질수록 기하급수적으로 커지므로 최적화 필요

 

3.2. Dynamic Programming

• DP 기본 개념
  • i ~ k 범위에서의 최소곱셈 & k + 1 ~ j까지의 범위에서의 최소 곱셈
  • 그 둘을 곱하는 곱셈의 횟수

- example

- 최적 순서의 구축

-> M[i][j]를 구하기 위해서는 M[i][k]와 M[k+1][j]가 이미 구해져 있어야 함

- 시간복잡도

• every case ∈ Θ(n^3)

 

4. 최적 이진검색 트리

• Optimal Binary Search Tree: 키를 찾는데 걸리는 평균시간이 최소가 되도록 구축된 트리
• 각 키를 찾을 확률이 주어져 있을 때(모두 같지 않음), 키를 찾는데 걸리는 평균시간이 최소가 되도록 이진트리를 구축하는 문제
• notation
  • p_i = key_i의 검색 빈도 -> 얼마나 자주 검색되는지
  • c_i = 주어진 트리에서 Key_i를 찾는데 필요한 비교횟수
  • 평균검색시간 = Σ(c_i * p_i)

-> DP에서는 매 단계가 1층 기준이므로, c_i = 1 ->> Σp_i

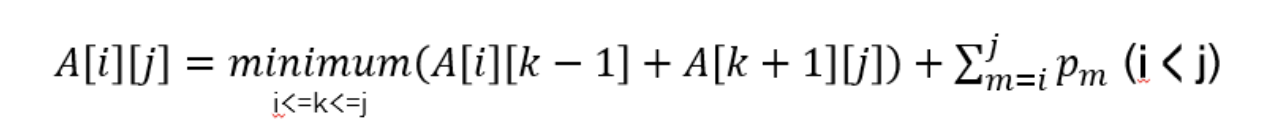
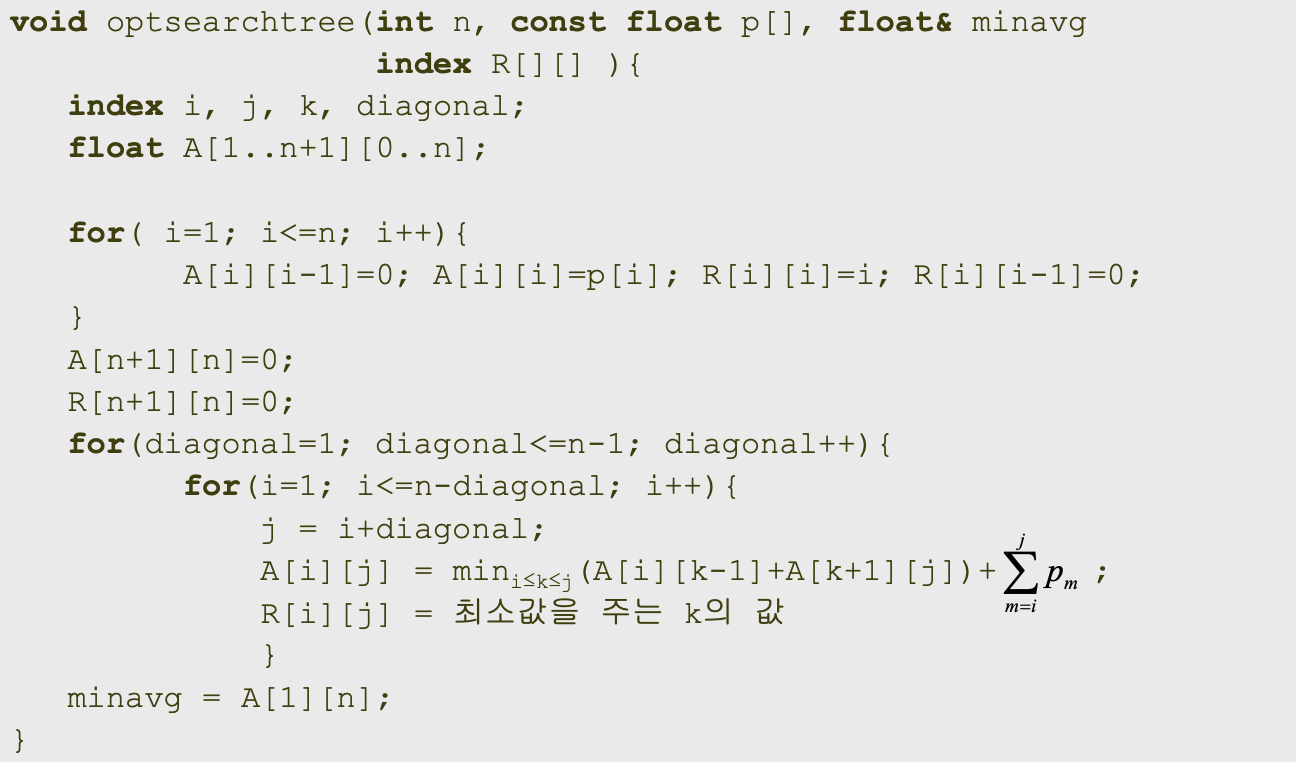
-> 일반화 버전

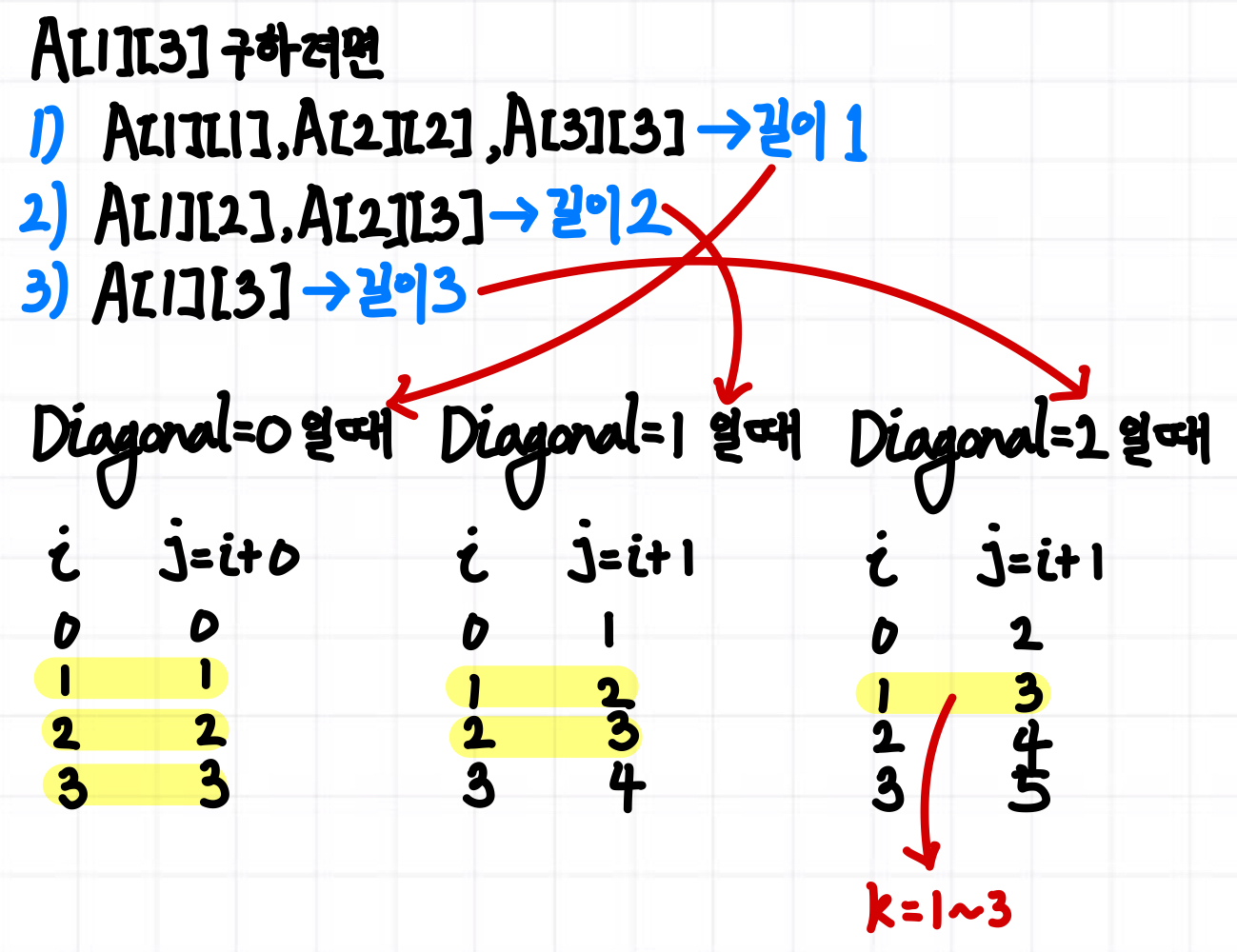
-> 해당 일반화 식을 이용하여 표를 채운 이후, A[1][n]을 구하면, 해당 값이 최적값

 

• A 배열: 최적 BST의 평균 검색 시간 -> 최적 BST의 모양은 알 수 없음
• R 배열: A 배열에 최적값을 넣는 순간 k의 값 -> 루트 노드가 k(좌측 서브트리가 1~k-1, 우측 서브트리가 k+1 ~ n)

 

 

5. DNA 서열 맞춤(sequence alignment)

• 동족서열(homologous sequence)
  • 하나의 종에서 출발하여, 교환, 삽입, 삭제 돌연변이에 의해 서열이 달라짐
  • 달라진 두 종에서 추출한 염기서열을 동족서열이라 함
  • 이 두 서열이 얼마나 다른지를 확인해서, 종족 간의 거리를 측정
  • 두 개의 염기서열을 어떻게 맞춰야 할까?
• DNA 서열 맞춤 문제: 두 개의 서열을 최소비용으로 맞추는 방법을 찾는다.

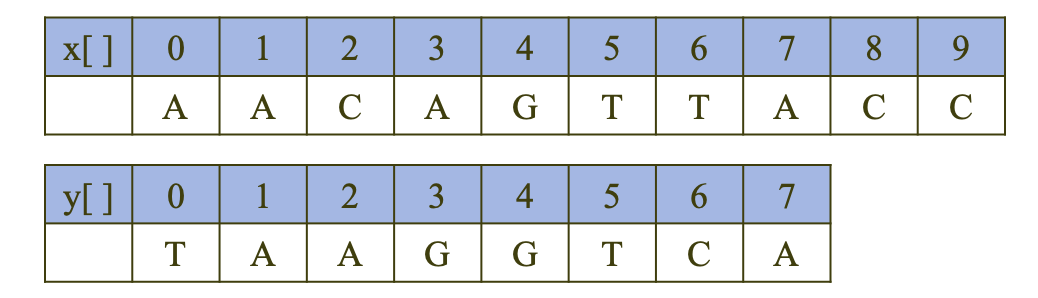
• opt(i, j): 부분 서열 x[i, ..., 9]와 y[j, ..., 7]의 최적 맞춤 비용
• opt(0, 0): 부분 서열 x[0, ..., 9]와 y[0, ..., 7]의 최적 맞춤 비용 -> 구하려는 최종 비용

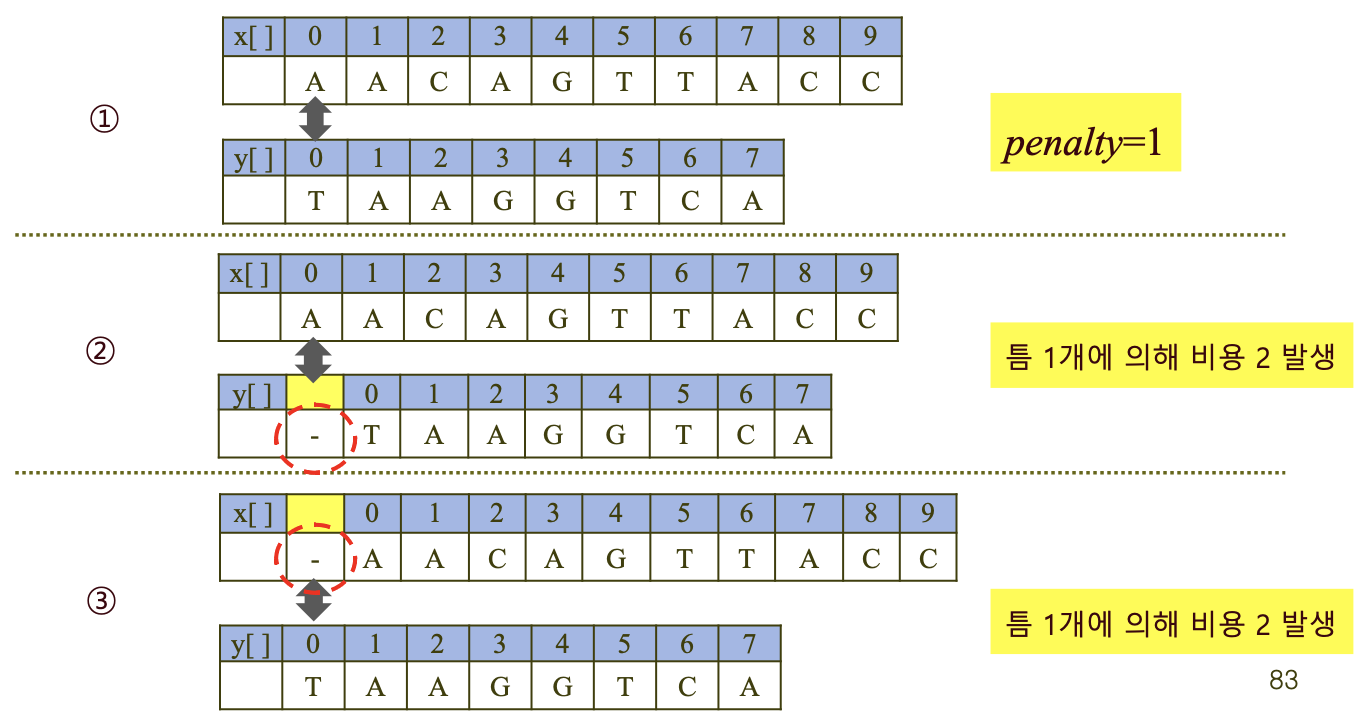
• 둘을 맞추는 경우 -> penalty = 0
• 못 맞추는 경우 -> penalty = 1
• y쪽을 틈으로 비워두는 경우 -> +2
• x쪽을 틈으로 비워두는 경우 -> +2

- Divide-and-Conquer 구현

-> 중복호출하는 경우가 너무 많아 비효율적

 

- Dynamic Programming

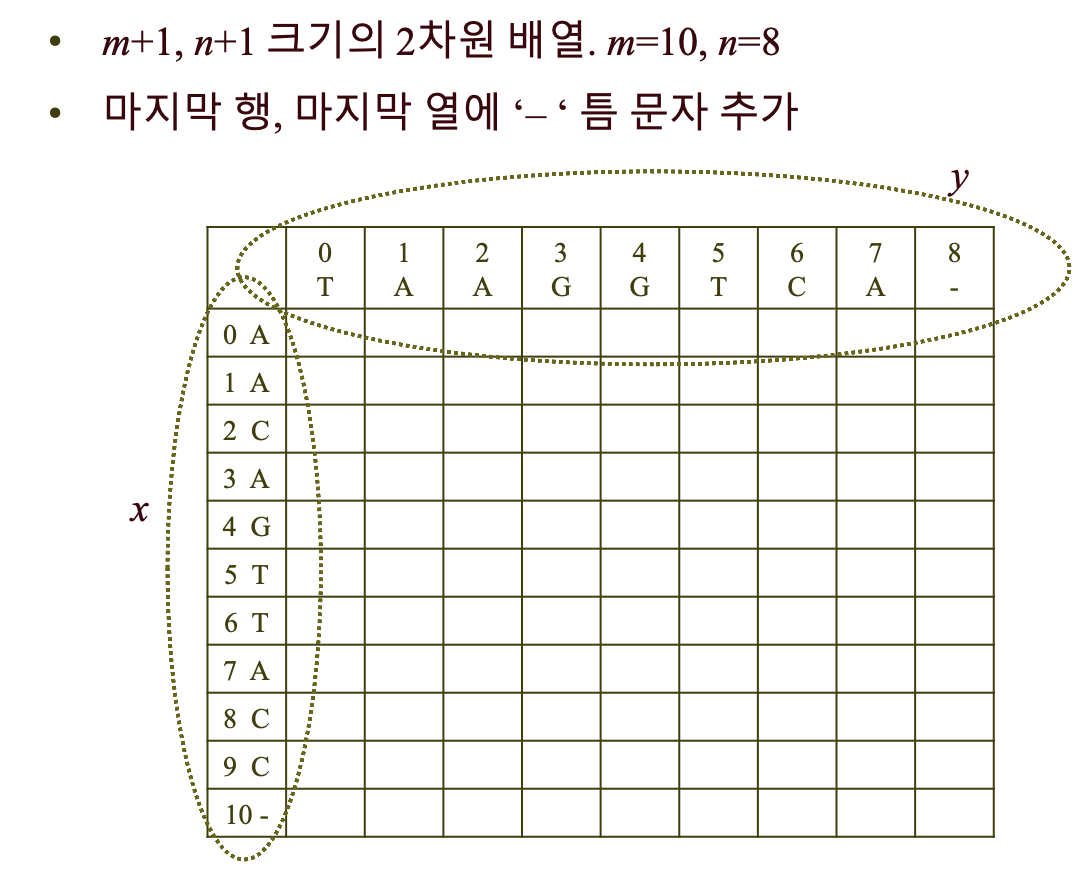
1. 틈 행과 틈 열을 채워 넣음

2. 우측 아래부터 대각원소들을 채워 넣음

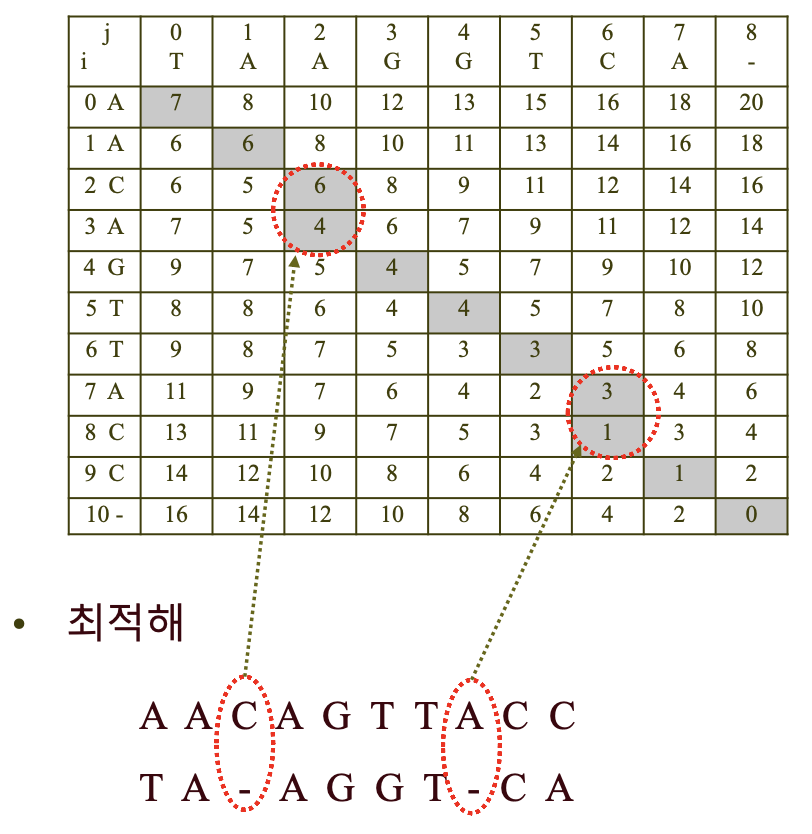
>> 최적서열맞춤 찾아가는 방법

1. [0][0] 선택
2. 경로에 넣을 둘째 항목을 찾는다
   1. [0][1] 검사
   2. [1][0] 검사
   3. [1][1] 검사

>> 맞춤된 서열을 구성하는 방법

1. 최적배열의 오른쪽 맨 아래 구성에서 시작하여 표시해둔 경로를 따라감
2. 배열의 [i][j]칸에 도달하기 위해서 대각선으로 이동할 때 마다,
   • i번째 행에 해당하는 문자를 x서열에 넣고
   • j번째 행에 해당하는 문자를 y 서열에 넣음
3. 배열의 [i][j]칸에 도달하기 위해서 위로 이동할 때 마다,
   • i번째 행에 해당하는 문자를 x서열에 넣고
   • 틈 문자를 y서열에 넣음
4. 배열의 [i][j]칸에 도달하기 위해서 아래로 이동할 때 마다
   • 틈 문자를 x서열에 넣고
   • j번째 행에 해당하는 문자를 y서열에 넣음

 

---

참고자료

• https://gsmesie692.tistory.com/116

최적 이진 탐색 트리 (Optimal Binary Search Tree)