| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- PCA
- Machine Learning
- OpenAI
- 지도학습
- LG
- supervised learning
- 티스토리챌린지
- Classification
- 회귀
- 머신러닝
- regression
- AI
- 딥러닝
- 오블완
- deep learning
- 해커톤
- LLM
- LG Aimers
- ChatGPT
- GPT-4
- 분류
- gpt
- LG Aimers 4th
Archives
- Today
- Total
SYDev
[Data Structure] Chapter 01: 자료구조와 알고리즘 본문
Data Structure & Algorithm/Data Structure
[Data Structure] Chapter 01: 자료구조와 알고리즘
시데브 2023. 8. 6. 16:29자료구조와 알고리즘에 대한 기본적인 개념을 이해하고, 알고리즘의 성능분석 방법에 대해 알아보자.
자료구조
- 프로그램이란 데이터를 표현하고, 그렇게 표현된 데이터를 처리하는 것이다.
- 여기서 데이터의 표현은 데이터의 저장을 포함하는 개념이고, 이런 데이터의 저장을 담당하는 것이 자료구조이다.
쉽게 말해서 자료구조란, 데이터 값의 모임, 또 데이터 간의 관계, 그리고 데이터에 적용할 수 있는 함수나 명령을 의미한다.
자료구조 종류
| 선형구조 | 비선형구조 | 파일구조 | 단순구조 |
| 리스트 | 트리 | 순차파일 | 정수 |
| 스택 | 그래프 | 색인파일 | 실수 |
| 큐 | 직접파일 | 문자 | |
| 문자열 |
자료구조와 알고리즘
- 알고리즘은 표현 및 저장된 데이터를 대상으로하는 '문제 해결 방법'을 뜻한다.
- 알고리즘은 자료구조에 의존적이다. 자료구조의 형태에 따라 알고리즘의 선택이 달라진다.
int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; //자료구조적 측면의 코드
for(idx=0; idx<10; idx++) //배열 arr과 변수 sum, idx가 선언되었다 가정.
sum+= arr[idx]; //알고리즘적 측면의 코드
알고리즘의 성능분석 방법
시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)
- 알고리즘을 평가하는 두 가지 요소는 속도와 메모리의 사용량이다.
- 시간 복잡도: 속도에 해당하는 알고리즘의 분석결과
- 공간 복잡도: 메모리 사용량에 대한 분석결과
- 보통은 알고리즘 성능을 평가할 때 ,시간 복잡도에 초점을 두어 판단한다.
알고리즘의 속도를 측정하는 방법
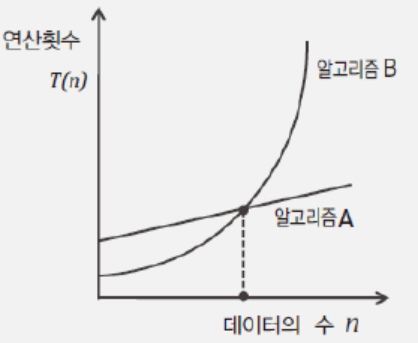
- 처리해야 할 데이터의 수 n에 대한 연산횟수의 함수 $T(n)$을 구성하고, 연산횟수를 통해서 알고리즘의 빠르기를 판단한다.
- 식을 구성하면 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단할 수 있다.
순차 탐색(Linear Search) 알고리즘과 시간 복잡도 분석의 핵심요소
다음은 순차 탐색 알고리즘을 적용한 예시이다.
#include <stdio.h>
int LSearch(int ar[], int len, int target) //순차 탐색 알고리즘 적용된 함수
{
int i;
for(i=0; i<len; i++)
{
if(ar[i]==target)
return i; //찾은 대상의 인덱스 값 변환
}
return -1; //찾지 못했음을 의미하는 값 반환
}
int main(void)
{
int arr[] = {3, 5, 2, 4, 9};
int idx;
idx = LSearch(arr, sizeof(arr)/sizeof(int), 4);
if(idx==-1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스: %d \n", idx);
/*
%d: 부호 있는 정수형
%c: 문자열 하나
%p: 주소(16진수)
%x: 정수(16진수) -> 알파벳 소문자
%X: 정수(16진수) -> 알파벳 대문자
*/
idx = LSearch(arr, sizeof(arr)/sizeof(int), 7);
if(idx == -1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스: %d \n", idx);
return 0;
}타겟 저장 인덱스: 3
탐색 실패- 알고리즘의 핵심이 되는 연산을 찾아 시간 복잡도를 분석해야 한다.
- ++, < 연산이 ==연산자에 의존적이기 때문에, ==연산자의 수행 횟수를 대상으로 시간 복잡도를 분석
- 알고리즘마다 최선의 경우(best case), 평균적인 경우(average case), 최악의 경우(worst case)가 있는데, 보통 알고리즘의 평가에는 최악의 경우가 기준이 된다.
순차 탐색 알고리즘의 시간 복잡도 계산: 최악의 경우(worst case)
- 데이터의 수가 n개일 때, 최악의 경우에 해당하는 연산횟수는 n이다.
- 따라서 데이터 수 n에 대한 연산횟수의 함수 T(n)은 다음과 같다. $T(n) = n$
이진 탐색(Binary Search) 알고리즘
- 배열을 대상으로 이진 탐색 알고리즘을 적용하려면 "배열에 저장된 데이터를 정렬되어 있어야 한다."라는 조건을 만족해야 한다.
#include <stdio.h>
int BSearch(int ar[], int len, int target)
{
int first=0; //탐색 대상의 시작 인덱스 값
int last=len-1; //탐색 대상의 마지막 인덱스 값
int mid;
while(first <= last)
{
mid=(first+last)/2; //탐색 대상의 중앙을 찾는다.
if(target == ar[mid]) //중앙에 저장된 것이 타겟이라면
{
return mid; //탐색 완료!
}
else //타겟이 아니라면 탐색 대상을 반으로 줄인다.
{
if(target<ar[mid])
last=mid-1; //새로운 탐색의 범위에서 mid의 배열요소 제외
else
first=mid+1; //새로운 탐색의 범위에서 mid의 배열요소 제외
}
}
return -1; //찾지 못했을 때 반환되는 값 -1
}
int main(void)
{
int arr[] = {1, 3, 5, 7, 9};
int idx;
idx = BSearch(arr, sizeof(arr)/sizeof(int), 7);
if(idx==-1)
printf("탐색 실패\n");
else
printf("타겟 저장 인덱스: %d \n", idx);
idx = BSearch(arr, sizeof(arr)/sizeof(int), 4);
if(idx==-1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스: %d \n", idx);
return 0;
}타겟 저장 인덱스: 3
탐색 실패
이진 탐색 알고리즘의 시간 복잡도 계산: 최악의 경우(worst case)
- ==연산(비교연산)이 해당 알고리즘의 핵심 연산
- n이 1이 되기까지 2로 나눈 횟수(k회)만큼 비교연산 진행
- 데이터가 1개 남았을 때, 추가적으로 비교연산 1회 진행
$T(n) = k+1$
$n*(1/2)^k = 1$ -> n이 1이 되기까지 나눈 횟수 k
$n = 2^k$
$log_2 n = k$
$∴ T(n) = log_2 n + 1$
빅-오 표기법(Big-Oh Notation)
두 개의 함수 $f(n)$과 $g(n)$이 주어졌을 때, 모든 n ≥ K에 대하여 f(n) ≤ Cg(n)을 만족하는 두 개의 상수 $C$와 $K$가 존재하면, $f(n)$의 빅-오는 $O(g(n))$이다.
- 위와 같이 복잡한 정의를 따르지 않아도, 식에서 큰 비율을 차지하는 항을 남겨 간략화하면 된다. -> 근사치식
- 빅-오 표기법에 따르면 $T(n) = log_2 n + 1$에서 데이터의 양이 많아질수록 1은 의미가 없어지므로 $T(n) = log_2 n$으로 간략화할 수 있고, 빅-오 표기법으로 표현하면 $T(n)$의 빅-오는 $O(log_2 n)$이다.
대표적인 빅-오
- $O(1)$: 상수형 빅-오, 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘을 의미한다.
- $O(log n)$: 로그형 빅-오, '데이터 수의 증가율'에 비해서 '연산횟수의 증가율'이 훨씬 낮은 알고리즘을 의미한다.
- $O(n)$: 선형 빅-오, 데이터의 수와 연산횟수가 비례하는 알고리즘을 의미한다.
- $O(nlog n)$ : 선형로그형 빅-오, 데이터의 수가 두 배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘을 의미한다.
- $O(n^2)$ : 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다.
- $O(n^3)$ : 데이터 수의 세 제곱에 해당하는 연산횟수를 요구하는 알고리즘을 의미한다.

순차 탐색 알고리즘과 이진 탐색 알고리즘의 비교
#include <stdio.h>
int BSearch(int ar[], int len, int target)
{
int first = 0;
int last = len-1;
int mid;
int opCount = 0; //비교연산의 횟수를 기록
while(first<=last)
{
mid = (first+last) / 2;
if(target == ar[mid])
{
return mid;
}
else
{
if(target<ar[mid])
last = mid-1;
else
first = mid+1;
}
opCount +=1; //비교연산의 횟수 1 증가
}
printf("비교연산횟수: %d \n", opCount);
return -1;
}
int main(void)
{
int arr1[500] = {0,}; //모든 요소 0으로 초기화
int arr2[5000] = {0,}; //모든 요소 0으로 초기화
int arr3[50000] = {0,}; //모든 요소 0으로 초기화
int idx;
// 배열 arr1을 대상으로, 저장되지 않은 정수 1을 찾으라고 명령
idx = BSearch(arr1, sizeof(arr1)/sizeof(int), 1);
if(idx == -1)
printf("탐색 실패 \n\n");
else
printf("타겟 저장 인덱스: %d \n", idx);
// 배열 arr2를 대상으로, 저장되지 않은 정수 2를 찾으라고 명령
idx = BSearch(arr2, sizeof(arr2)/sizeof(int), 2);
if(idx == -1)
printf("탐색 실패 \n\n");
else
printf("타겟 저장 인덱스: %d \n", idx);
// 배열 arr3을 대상으로, 저장되지 않은 정수 3을 찾으라고 명령
idx = BSearch(arr3, sizeof(arr3)/sizeof(int), 3);
if(idx == -1)
printf("탐색 실패 \n\n");
else
printf("타겟 저장 인덱스: %d \n", idx);
return 0;
}비교연산횟수: 9
탐색 실패
비교연산횟수: 13
탐색 실패
비교연산횟수: 16
탐색 실패- $O(n)$인 순차 탐색 알고리즘의 경우 데이터 수가 500, 5000, 50000일 때 비교연산의 횟수는 500, 5000, 50000이다.
- 위 예제에 따르면, $O(log_2 n)$인 순차 탐색 알고리즘의 경우 데이터 수가 500, 5000, 50000일 때 비교연산의 횟수는 약 9, 13, 16이다.
| n | 순차 탐색 연산횟수 | 이진 탐색 연산횟수 |
| 500 | 500 | 9 |
| 5,000 | 5,000 | 13 |
| 50,000 | 50,000 | 16 |
참고자료
- 윤성우, <윤성우의 열혈 자료구조>, 오렌지미디어, 2022.04.11
- https://ko.wikipedia.org/wiki/%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0
자료 구조 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 해시 테이블로 알려진 자료 구조 이진 트리의 예 자료구조(資料構造, 영어: data structure)는 컴퓨터 과학에서 효율적인 접근 및 수정을 가능케 하는 자료의 조직,
ko.wikipedia.org
점근 표기법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 점근 표기법(漸近 表記法, 영어: asymptotic notation)은 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 수론과 해석학의 방법이다. 알고리즘의 복잡도를
ko.wikipedia.org
[Data Structures][01-2] 알고리즘의 성능 분석 방법
본 글은 윤성우의 열혈 자료구조 책을 읽고, 강의를 수강하고 복습한 것을 기록한 글입니다. 강의 교안 또한 참고하여 작성하였습니다. (강의 교안의 경우 오렌지 미디어에서 다운로드할 수 있
valuelog.tistory.com
728x90
반응형
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] Chapter 05: 원형, 양방향 연결 리스트 (0) | 2023.08.12 |
|---|---|
| [Data Structure] Chapter 04: 연결 리스트의 이해와 구현 (0) | 2023.08.11 |
| [Data Structure] Chapter 03: 추상 자료형과 배열 기반 리스트 (0) | 2023.08.09 |
| C언어에서의 구조체와 typedef (0) | 2023.08.08 |
| [Data Structure] Chapter 02: 재귀(Recursion) (0) | 2023.08.07 |


