| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 회귀
- PCA
- 티스토리챌린지
- OpenAI
- 해커톤
- AI
- supervised learning
- regression
- GPT-4
- Classification
- 분류
- LG
- ChatGPT
- LLM
- 머신러닝
- Machine Learning
- 오블완
- LG Aimers
- 지도학습
- deep learning
- gpt
- 딥러닝
- LG Aimers 4th
Archives
- Today
- Total
SYDev
[Data Structure] Chapter 08: 트리(Tree) 본문
Data Structure & Algorithm/Data Structure
[Data Structure] Chapter 08: 트리(Tree)
시데브 2023. 8. 23. 15:16계층적 관계(Hierarchical Relationship)를 표현하는 자료구조인 트리(Tree)를 이해하고,
트리를 대표하는 이진트리를 이용해 수식 트리를 구현해보자.
트리
- 트리(Tree): 트리는 계층적 관계(Hierarchical Relationship)를 표현하는 자료구조이다.
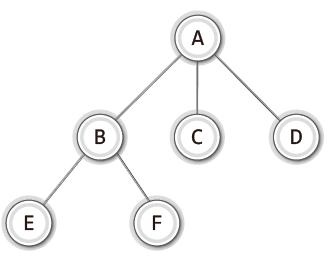

- 노드(node): 트리의 구성요소에 해당하는 A, B, C, D, E, F와 같은 요소
- 간선(edge): 노드와 노드를 연결하는 연결선
- 루트 노드(root node): 트리 구조에서 최상위에 존재하는 A와 같은 노드
- 단말 노드(terminal node): 아래로 또 다른 노드가 연결되어 있지 않은 E, F, C, D와 같은 노드
- 내부 노드(internal node): 단말 노드를 제외한 모든 노드로 A, B와 같은 노드
- 레벨(level): 각 층별로 숫자를 매겨서, 이를 트리의 '레벨'이라 칭한다.
- 높이(height): 트리의 최고 레벨을 가리켜 '높이'라 한다.
- 노드 A는 노드 B, C, D의 parent node이다.
- 노드 B, C, D는 노드 A의 child node이다.
- 노드 B, C, D는 부모 노드가 같으므로, 서로 sibling node이다.
서브 트리
- 서브 트리(sub tree): 큰 트리에 속하는 작은 트리를 뜻한다.

이진 트리
- 이진 트리는 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
- 이진 트리는 나뉘어진 두 서브 트리도 모두 이진 트리여야 한다.
- 노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면, 공집합(empty set) 노드가 존재하는 것으로 간주한다.

포화 이진 트리와 완전 이진 트리
- 포화 이진 트리(full binary tree): 모든 레벨이 꽉 찬 이진 트리를 의미한다.
- 완전 이진 트리(complete binary tree): 노드가 빈 틈 없이 채워진 이진 트리를 의미한다.
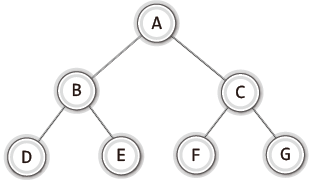
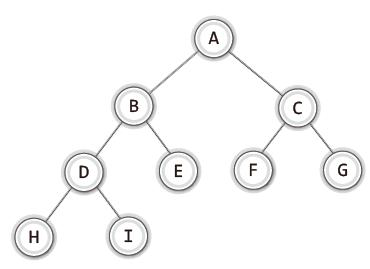
배열 기반 이진 트리의 구현

- 노드 번호를 기준으로 데이터가 저장되는 배열의 위치를 결정한다.
연결 리스트 기반 이진 트리의 구현
- 연결 리스트 기반의 구성 형태가 트리와 일치하기 때문에 구현하기 용이하다.

이진 트리 자료구조의 ADT
BTreeNode * MakeBTreeNode(void);
- 이진 트리 노드를 생성하여 그 주소 값을 반환한다.
BTData GetData(BtreeNode * bt);
- 노드에 저장된 데이터를 반환한다.
void SetData(BTreeNode * bt, BTData data);
- 노드에 데이터를 저장한다. data로 전달된 값을 저장한다.
BTreeNode * GetLeftSubTree(BTreeNode * bt);
- 왼쪽 서브 트리의 주소 값을 반환한다.
BTreeNode * GetRightSubTree(BTreeNode * bt);
- 오른쪽 서브 트리의 주소 값을 반환한다.
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
- 왼쪽 서브 트리를 연결한다
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
- 오른쪽 서브 트리를 연결한다
파일명: BinaryTree.h
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endif
파일명: BinaryTree.c
#include "BinaryTree.h"
#include <stdio.h>
#include <stdlib.h>
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * newNode = (BTreeNode*)malloc(sizeof(BTreeNode));
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
파일명: BinaryTreeMain.c
#include <stdio.h>
#include "BinaryTree.h"
int main(void)
{
BTreeNode * bt1 = MakeBTreeNode();
BTreeNode * bt2 = MakeBTreeNode();
BTreeNode * bt3 = MakeBTreeNode();
BTreeNode * bt4 = MakeBTreeNode();
SetData(bt1, 1);
SetData(bt2, 2);
SetData(bt3, 3);
SetData(bt4, 4);
MakeLeftSubTree(bt1, bt2);
MakeRightSubTree(bt1, bt3);
MakeLeftSubTree(bt2, bt4);
printf("%d \n", GetData(GetLeftSubTree(bt1)));
printf("%d \n", GetData(GetLeftSubTree(GetLeftSubTree(bt1))));
return 0;
}2
4
이진 트리의 순회
순회의 세 가지 방법
- 전위 순회(Preorder Traversal)
- 중위 순회(Inorder Traversal)
- 후위 순회(Postorder Traversal)

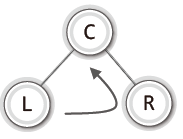
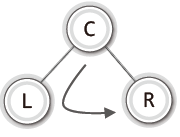
순회의 재귀적 표현
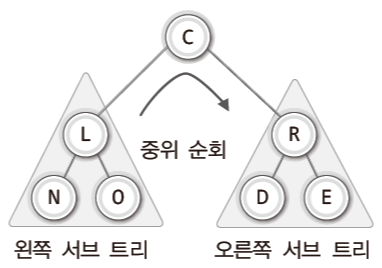
- 1단계: 왼쪽 서브 트리의 순회
- 2단계: 루트 노드의 방문
- 3단계: 오른쪽 서브 트리의 순회
파일명: BinaryTree2.h
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
void DeleteTree(BTreeNode * bt);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
typedef void (*VisitFuncPtr)(BTData data);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);
#endif
파일명: BinaryTree2.c
#include "BinaryTree2.h"
#include <stdio.h>
#include <stdlib.h>
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * newNode = (BTreeNode*)malloc(sizeof(BTreeNode));
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
void DeleteTree(BTreeNode * bt)
{
if(bt->data == NULL)
return;
DeleteTree(bt->left);
DeleteTree(bt->right);
free(bt);
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
action(bt->data);
PreorderTraverse(bt->left, action);
PreorderTraverse(bt->right, action);
}
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
InorderTraverse(bt->left, action);
action(bt->data);
InorderTraverse(bt->right, action);
}
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
PostorderTraverse(bt->left, action);
PostorderTraverse(bt->right, action);
action(bt->data);
}
파일명: BinaryTreeMain2.c
#include <stdio.h>
#include "BinaryTree2.h"
void ShowIntData(int data);
int main(void)
{
BTreeNode * bt1 = MakeBTreeNode();
BTreeNode * bt2 = MakeBTreeNode();
BTreeNode * bt3 = MakeBTreeNode();
BTreeNode * bt4 = MakeBTreeNode();
BTreeNode * bt5 = MakeBTreeNode();
BTreeNode * bt6 = MakeBTreeNode();
SetData(bt1, 1);
SetData(bt2, 2);
SetData(bt3, 3);
SetData(bt4, 4);
SetData(bt5, 5);
SetData(bt6, 6);
MakeLeftSubTree(bt1, bt2);
MakeRightSubTree(bt1, bt3);
MakeLeftSubTree(bt2, bt4);
MakeRightSubTree(bt2, bt5);
MakeRightSubTree(bt3, bt6);
PreorderTraverse(bt1, ShowIntData);
printf("\n");
InorderTraverse(bt1, ShowIntData);
printf("\n");
PostorderTraverse(bt1, ShowIntData);
printf("\n");
return 0;
}
void ShowIntData(int data)
{
printf("%d ", data);
}1 2 4 5 3 6
4 2 5 1 3 6
4 5 2 6 3 1
수식 트리의 구현
- 문자열 형태의 수식을 수식 트리로 표현하면 컴파일러의 수식해석이 좋아진다.

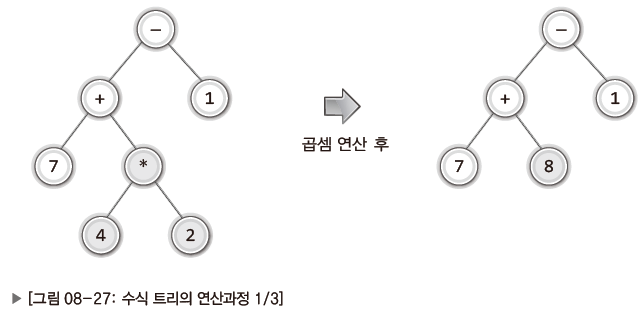
- 연산의 결과가 연산자 노드 자리를 대체하는 방식으로 진행된다.
- 후위 표기법이 수식 트리 형태로 바꾸기 용이하다.
- 따라서, 중위 표기법의 수식 -> 후위 표기법의 수식 -> 수식 트리 순서로 수식 트리를 구현하는 것이 좋다.
- 수식 트리를 구현하기 위해서는 이진 트리, 스택 자료구조가 필요하다.
- 같은 경로에 이전에 구현한 BinaryTree2.h,BinaryTree2.c, ListBaseStack.h,ListBaseStack.c를 포함하여 구현하겠다.
파일명: ExpressionTree.h
#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[]); //수식 트리 구성
int EvaluateExpTree(BTreeNode * bt); //수식 트리 계산
void ShowPrefixTypeExp(BTreeNode * bt); //전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode * bt); //중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode * bt); //후위 표기법 기반 출력
#endif
파일명: ExpressionTree.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>
#include "ListBaseStack.h"
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[])
{
Stack stack;
BTreeNode * pnode;
int expLen = strlen(exp);
int i;
StackInit(&stack);
for(i=0; i<expLen; i++)
{
pnode = MakeBTreeNode();
if (isdigit(exp[i]))
{
SetData(pnode, exp[i] - '0');
}
else
{
MakeRightSubTree(pnode, SPop(&stack));
MakeLeftSubTree(pnode, SPop(&stack));
SetData(pnode, exp[i]);
}
SPush(&stack, pnode);
}
return SPop(&stack);
}
int EvaluateExpTree(BTreeNode * bt)
{
int op1, op2;
if(GetLeftSubTree(bt)==NULL && GetRightSubTree(bt)==NULL)
return GetData(bt);
op1=EvaluateExpTree(GetLeftSubTree(bt));
op2=EvaluateExpTree(GetRightSubTree(bt));
switch(GetData(bt))
{
case '+':
return op1+op2;
case '-':
return op1-op2;
case '*':
return op1*op2;
case '/':
return op1/op2;
}
}
void ShowNodeData(int data) //함수 포인터 매개변수로 전달될 함수
{
if(0<data && data<=9)
printf("%d ", data);
else
printf("%c ", data);
}
void ShowPrefixTypeExp(BTreeNode * bt)
{
PreorderTraverse(bt, ShowNodeData);
}
void ShowInfixTypeExp(BTreeNode * bt)
{
InorderTraverse(bt, ShowNodeData);
}
void ShowPostfixTypeExp(BTreeNode * bt)
{
PostorderTraverse(bt, ShowNodeData);
}
파일명: ExpressionTreeMain.c
#include <stdio.h>
#include "ExpressionTree.h"
int main(void)
{
char exp[] = "12+7*";
BTreeNode * eTree = MakeExpTree(exp);
printf("전위 표기법의 수식: ");
ShowPrefixTypeExp(eTree); printf("\n");
printf("중위 표기법의 수식: ");
ShowInfixTypeExp(eTree); printf("\n");
printf("후위 표기법의 수식: ");
ShowPostfixTypeExp(eTree); printf("\n");
printf("연산의 결과: %d \n", EvaluateExpTree(eTree));
return 0;
}전위 표기법의 수식: * + 1 2 7
중위 표기법의 수식: 1 + 2 * 7
후위 표기법의 수식: 1 2 + 7 *
연산의 결과: 21
문제 08-2
더보기
void ShowInfixTypeExp(BTreeNode * bt)
{
if(bt==NULL)
return;
if(bt->left!=NULL || bt->right!=NULL)
printf("( ");
ShowInfixTypeExp(bt->left);
ShowNodeData(bt->data);
ShowInfixTypeExp(bt->right);
if(bt->left != NULL || bt->right != NULL)
printf(") ");
}
함수를 위와 같이 바꿔주면 된다.
참고자료
- 윤성우, <윤성우의 열혈 자료구조>, 오렌지미디어, 2022.04.11
728x90
반응형
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] Chapter 10-1: 단순한 정렬 알고리즘 (0) | 2023.09.08 |
|---|---|
| [Data Structure] Chapter 09: 우선순위 큐(Priority Queue)와 힙(Heap) (1) | 2023.09.01 |
| [Data Structure] Chapter 07: 큐(Queue) (0) | 2023.08.16 |
| [Data Structure] Chapter 06: 스택(Stack) (0) | 2023.08.15 |
| [Data Structure] Chapter 05: 원형, 양방향 연결 리스트 (0) | 2023.08.12 |




