| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- supervised learning
- deep learning
- LG Aimers 4th
- 딥러닝
- ChatGPT
- PCA
- gpt
- AI
- 오블완
- 분류
- Classification
- 지도학습
- LG
- 티스토리챌린지
- 머신러닝
- GPT-4
- 해커톤
- Machine Learning
- regression
- 회귀
- OpenAI
- LLM
- LG Aimers
- Today
- Total
SYDev
[알고리즘 문제 해결 전략] Chapter 7. 분할 정복 본문
가장 유명한 알고리즘 디자인 패러다임인 분할 정복(Divide & Conquer)을
이해하고 예제를 통해 구현해보자.
분할 정복
- 분할 정복(Divide & Conquer): 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 얻어내는 방법이다.
- 부분 문제와 나머지를 나눌 때 거의 같은 크기로 나눈다.
분할 정복 설계
- divide: 문제를 더 작은 문제로 분할하는 과정
- conquer: 해결이 용이한 수준까지 분할된 문제를 해결하는 과정
- merge: 각 문제에 대해 구한 답을 원래 문제에 대한 답으로 병합하는 과정
수열의 빠른 합과 행렬의 빠른 제곱

#include <iostream>
using namespace std;
int fastSum(int n)
{
if(n == 1){
return 1;
}
if(n % 2 == 1){
return fastSum(n-1) + n;
}
return 2*fastSum(n/2) + (n/2)*(n/2);
}
시간 복잡도 분석

행렬의 거듭제곱

#include <iostream>
using namespace std;
class SquareMatrix;
SquareMatrix identity(int n);
SquareMatrix pow(const SquareMatrix& A, int m) {
if(m == 0) {
return identity(A.size());
}
if(m % 2 > 0){
return pow(A, m-1) * A;
}
SquareMatrix half = pow(A, m / 2);
return half * half;
}
시간 복잡도 분석
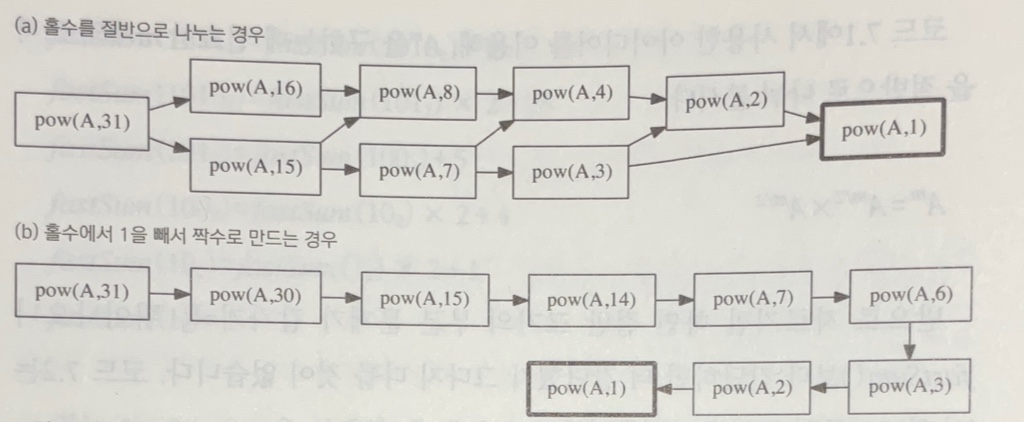
- 홀수일 때 절반으로 나누는 것이 빠를 것 같지만, 위 그림처럼 중복되는 연산이 많이 발생하여 계산 횟수가 m-1번 곱할 때와 차이가 별로 없어진다. -> overlapping subploblems
- (b)의 경우에 따라 호출 횟수는 O(lgm)
병합 정렬과 퀵 정렬
- 주어진 수열을 크기 순서대로 정렬하는 문제는 전산학에서 가장 유명한 문제 중 하나이다.
- 이 문제를 해결하는 알고리즘 중 대표적으로 병합 정렬(Merge sort)과 퀵 정렬(Quick sort)이 있다.
- 두 알고리즘 모두 분할 정복 패러다임을 기반으로 만들어졌다.
병합 정렬
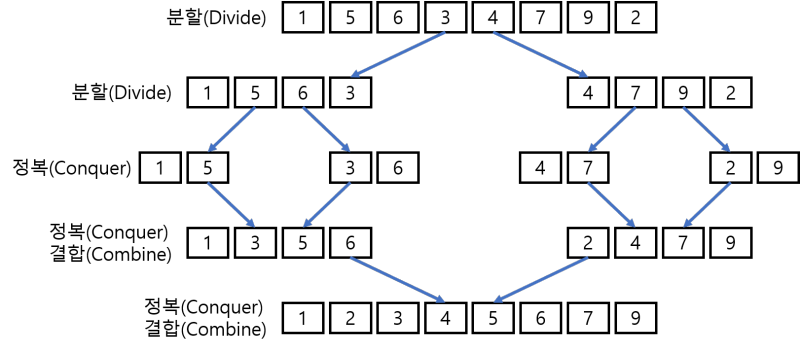
- 수열을 가운데에서 쪼개 비슷한 크기의 수열 두 개로 만든다.
- 이들을 재귀 호출을 이용해 각각 정렬한다.
- 이후 정렬된 배열을 하나로 합침으로써 정렬된 전체 수열을 얻는다.
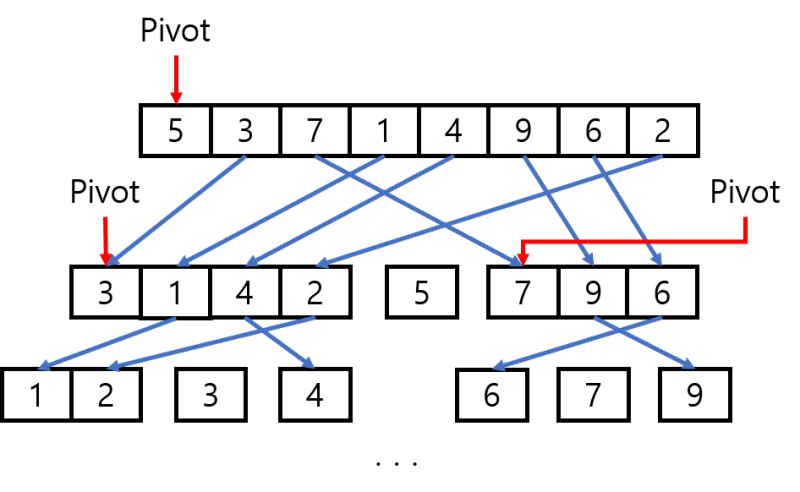
퀵 정렬
- 피벗을 이용하여 배열을 반으로 나누는 과정을 반복하여, 정렬을 진행하는 방법이다.
퀵 정렬에 대해서는 https://sypdevlog.tistory.com/135 <<해당 게시물에서 자세히 설명
시간 복잡도 분석
https://sypdevlog.tistory.com/135
[Data Structure] Chapter 10-2: 복잡하지만 효율적인 정렬 알고리즘
복잡하지만 효율적인 정렬 알고리즘에 대해 알아보자. 힙 정렬 이해와 구현 힙 정렬(Heap Sort): 힙 자료구조를 이용하여 정렬을 진행하는 알고리즘이다. #include #include "UsefulHeap.h" int PriComp(int n1, int
sypdevlog.tistory.com
- 병합 정렬 비교 연산: $O(nlogn)$, 이동 연산: $O(nlogn)$
- 퀵 정렬 시간복잡도: 최악의 경우 $O(n^2)$, 중간값 선택할 경우 $O(nlogn)$
카라츠바의 빠른 곱셈 알고리즘
- 수백, 수만 자리는 되는 큰 정수의 곱을 구할 때 사용하는 알고리즘이다.
두 정수의 곱을 구하는 일반적 알고리즘

//num[]의 자릿수 올림 처리
void normalize(vector<int>& num)
{
num.push_back(0);
for (int i = 0; i < num.size(); i++)
{
if (num[i] < 0) //음수인 경우의 처리 -> 카라츠바 구현 후 이해 가능
{
int borrow = (abs(num[i]) + 9) / 10;
num[i+1] -= borrow;
num[i] += borrow * 10;
}
else
{
num[i+1] += num[i] / 10;
num[i] %= 10;
}
}
while(num.size() > 1 && num.back() == 0) num.pop_back();
}
vector<int> multiply(const vector<int>& a, const vector<int> b)
{
vector<int> c(a.size() + b.size() + 1, 0); //가능한 최대 자릿수
for(int i = 0; i < a.size(); i++)
for(int j = 0; j < b.size(); i++)
c[i+j] += a[i] * b[j];
normalize(c);
return c;
}- n번 실행되는 for문이 두 번 겹쳐있기 때문에 시간 복잡도는 $O(n^2)$
카라츠바 곱셈 알고리즘
- 카라츠바 알고리즘은 곱셈 횟수를 줄이고 덧셈 뺄셈 연산 횟수를 늘려 시간 복잡도를 줄인다는 아이디어에서 시작한다!
- a와 b가 각각 256자리 수이고, a1과 b1은 첫 128자리, a0와 b0는 그 다음 128자리를 저장하도록 한다.
- 이때, 표현을 바꾸면 곱셈 연산 4번으로 표현한 식을 3번으로 바꿀 수 있다.
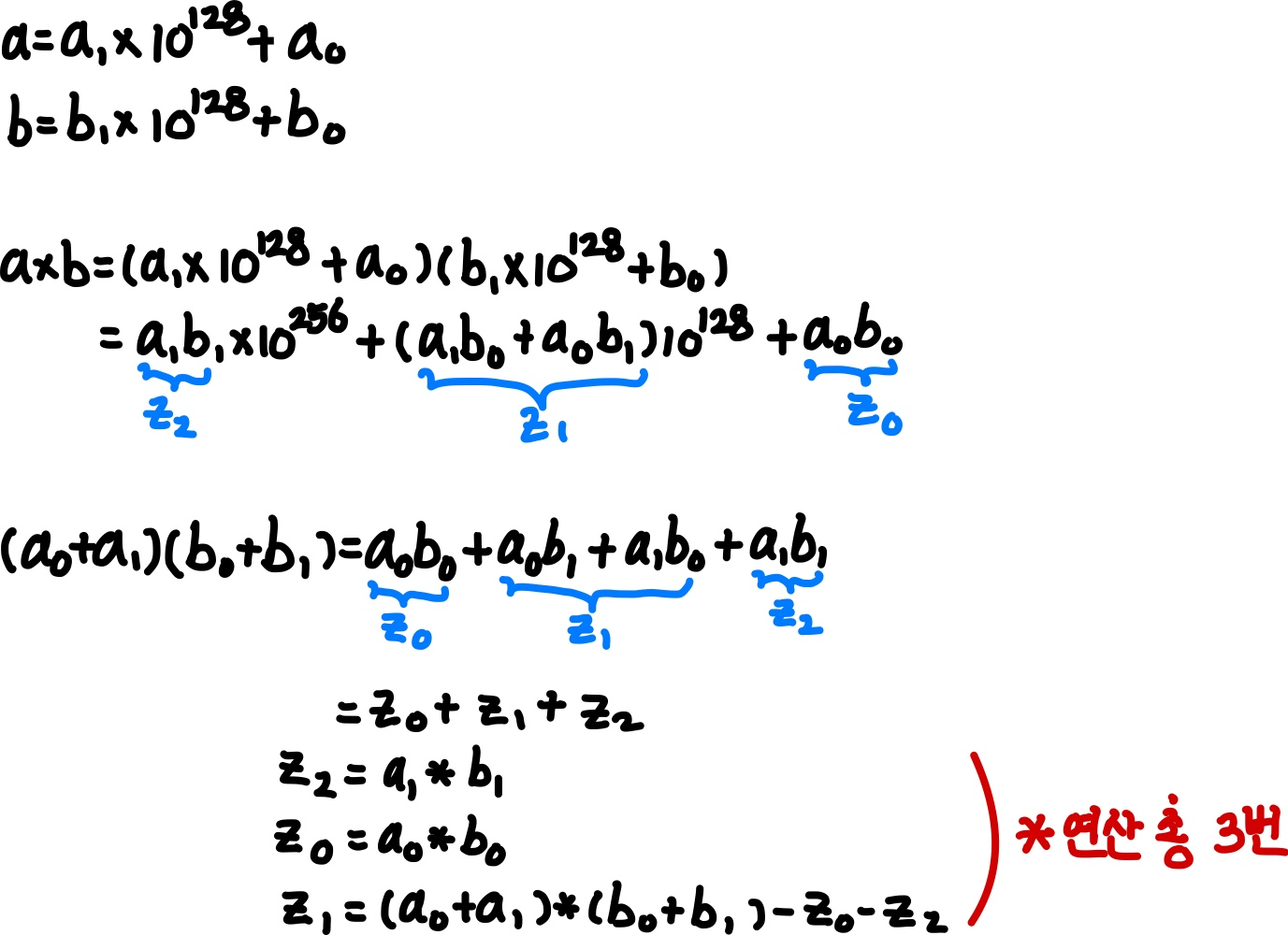
이를 코드로 구현하면 다음과 같다.
//a += b * (10^k);를 구현
void addTo(vector<int>& a, const vector<int>& b, int k);
//a -= b;를 구현 (a >= b 가정)
void subFrom(vector<int>& a, const vector<int>& b);
vector<int> karatsuba(const vector<int>& a, const vector<int>& b) {
int an = a.size(), bn = b.size();
//a가 b보다 짧을 경우 둘을 바꾼다.
if(an < bn) {
return karatsuba(b, a);
}
//base case: a나 b가 비어있는 경우
if(an == 0 || bn == 0) {
return vector<int>();
}
//base case: a가 비교적 짧은 경우 O(n^2) 곱셈으로 변경한다.
if(an <= 50) {
return multiply(a, b);
}
int half = an / 2;
vector<int> a0(a.begin(), a.begin() + half); //a.begin() ~ (a.begin() + half - 1)
vector<int> a1(a.begin() + half, a.end()); //(a.begin() + half) ~ (a.end() -1) -> a.end(): 끝 요소 + 1
vector<int> b0(b.begin(), b.begin() + min<int>(b.size(), half));
vector<int> b1(b.begin() + min<int>(b.size(), half), b.end());
vector<int> z2 = karatsuba(a1, b1);
vector<int> z0 = karatsuba(a0, b0);
//a0 = a0 + a1; b0 = b0 + b1;
addTo(a0, a1, 0);
addTo(b0, b1, 0);
//z1 = (a0 + a1)(b0 + b1) - z0 - z2;
vector<int> z1 = karatsuba(a0, b0);
subFrom(z1, z0);
subFrom(z1, z2);
//ret = z0 + z1 * 10^half + z2 * 10^(half/2)
vector<int> ret;
addTo(ret, z0, 0);
addTo(ret, z1, half);
addTo(ret, z2, half + half);
return ret;
}
시간 복잡도 분석
- 카라츠바 알고리즘의 시간 복잡도 분석은 병합 단계, 기저 사례의 두 부분으로 나눠서 판단해야 한다.

예제1: 쿼드 트리 뒤집기 (문제 ID: QUADTREE, 난이도: 하)
https://www.algospot.com/judge/problem/read/QUADTREE
algospot.com :: QUADTREE
쿼드 트리 뒤집기 문제 정보 문제 대량의 좌표 데이터를 메모리 안에 압축해 저장하기 위해 사용하는 여러 기법 중 쿼드 트리(quad tree)란 것이 있습니다. 주어진 공간을 항상 4개로 분할해 재귀적
www.algospot.com
#include <iostream>
#include <vector>
#include <string>
using namespace std;
string reverse(string::iterator& it)
{
char head = *it;
it++;
if(head == 'b' || head == 'w')
return string(1, head);
string upperLeft = reverse(it);
string upperRight = reverse(it);
string lowerLeft = reverse(it);
string lowerRight = reverse(it);
return string("x") + lowerLeft + lowerRight + upperLeft + upperRight;
}
int main(void)
{
int cases;
cin >> cases;
while(cases--)
{
string s;
cin >> s;
string::iterator it = s.begin();
cout << reverse(it) <<endl;
}
return 0;
}4
w
w
xbwwb
xwbbw
xbwxwbbwb
xxbwwbbbw
xxwwwbxwxwbbbwwxxxwwbbbwwwwbb
xxwbxwwxbbwwbwbxwbwwxwwwxbbwb>> 압축을 모두 풀고 뒤집기를 시행하기에는 input image size가 너무 거대하기 때문에, 압축을 다 풀지 않고 바로바로 뒤집기를 시행하는 방법을 택하는 것이 낫다.
시간 복잡도 분석
- reverse() 함수는 문자열의 한 글자 당 한 번씩 호출된다. 따라서 함수가 호출되는 횟수는 문자열의 길이에 비례하므로 시간 복잡도 O(n)이다.
배운 점
- iterator(반복자): 컨테이너 형식의 자료형 내부 요소를 가리키는 포인터와 유사한 객체이다. iterator가 참조형으로 전달되기 때문에 재귀 호출 내부에서 iterator를 옮기면 밖에서도 그 변화가 전달된다.
예제2: 울타리 잘라내기 (문제 ID: FENCE, 난이도: 중)
https://www.algospot.com/judge/problem/read/FENCE
algospot.com :: FENCE
울타리 잘라내기 문제 정보 문제 너비가 같은 N개의 나무 판자를 붙여 세운 울타리가 있습니다. 시간이 지남에 따라 판자들이 부러지거나 망가져 높이가 다 달라진 관계로 울타리를 통째로 교체
www.algospot.com
이 문제는 답안을 보기 전에 무식하게 풀기를 적용해서 풀어봤는데, 댓글에 있는 예제까지 모두 맞게 작동했지만 채점지에서는 오답으로 떴다.. 시간 초과 때문인지는 모르겠지만 아무튼 상당히 아쉬웠음.
#include <iostream>
#include <vector>
#include <string>
#include <cassert>
using namespace std;
int leftArea(const vector<int>& fence, int cur)
{
if(cur == 0)
return 0;
int area = 0;
for(int back = cur-1; back>=0; back--)
{
if(fence[back] < fence[cur])
break;
area += fence[cur];
}
return area;
}
int rightArea(const vector<int>& fence, int cur)
{
if(cur == fence.size() - 1)
return 0;
int area = 0;
for(int front = cur+1; front < fence.size() ; front++)
{
if(fence[front] < fence[cur])
break;
area += fence[cur];
}
return area;
}
int maxArea(const vector<int>& fence)
{
int answer = 0;
for(int cur = 0; cur < fence.size() - 1; cur++)
{
int curArea = leftArea(fence, cur) + rightArea(fence, cur) + fence[cur];
answer = max(curArea, answer);
}
return answer;
}
int main(void)
{
int cases;
cin >> cases;
assert(cases <= 50);
while(cases--)
{
int fenceNum;
cin >> fenceNum;
assert(fenceNum <= 20000 && fenceNum >= 1);
vector<int> fence(fenceNum);
for(int i = 0; i < fenceNum; i++)
{
cin >> fence[i];
assert(fence[i] <= 10000 && fence[i] >= 0);
}
cout << maxArea(fence) << endl;
}
return 0;
}3
7
7 1 5 9 6 7 3
20
7
1 4 4 4 4 1 1
16
4
1 8 2 2
8>> 모든 판자를 돌면서 해당 기점에서의 넓이를 비교해 최대값을 찾는 방법!
답안에서 쉽게 푼 방법!
//답안에서 쉽게 푼 방법
int bruteForce(const vector<int>& h)
{
int ret = 0;
int N = h.size();
//가능한 모든 left, right 조합 순회
for(int left = 0; left < N; left++)
{
int minHeight = h[left];
for(int right = left; right < N; right++)
{
minHeight = min(minHeight, h[right]);
ret = max(ret, (right - left + 1) * minHeight);
}
}
return ret;
}
int main(void)
{
int cases;
cin >> cases;
assert(cases <= 50);
while(cases--)
{
int fenceNum;
cin >> fenceNum;
assert(fenceNum <= 20000 && fenceNum >= 1);
vector<int> fence(fenceNum);
for(int i = 0; i < fenceNum; i++)
{
cin >> fence[i];
assert(fence[i] <= 10000 && fence[i] >= 0);
}
cout << bruteForce(fence) << endl;
}
return 0;
}3
7
7 1 5 9 6 7 3
20
7
1 4 4 4 4 1 1
16
4
1 8 2 2
8>> 모든 범위 경우의 수에서 넓이를 계산
#include <iostream>
#include <vector>
#include <string>
#include <cassert>
using namespace std;
//각 판자의 높이
//h[left..right]에서 구할 수 있는 가장 큰 사각형의 넓이
int solve(int left, int right, vector<int>& fence)
{
//판자가 하나만 있는 경우
if(left == right) return fence[left];
//[left, mid], [mid + 1, right]의 두 구간으로 분할
int mid = (left + right) / 2;
//case1, 2
int ret = max(solve(left, mid, fence), solve(mid+1, right, fence));
//case3
int lo = mid, hi = mid + 1;
int height = min(fence[lo], fence[hi]);
ret = max(ret, height * 2);
while(left < lo || hi < right)
{
if(hi < right && (lo == left || fence[lo - 1] < fence[hi + 1]))//오른쪽 height이 더 높을 때 right sie로
{
hi++;
height = min(height, fence[hi]);
}
else//왼쪽 hieght이 높을 때 left side로
{
lo--;
height = min(height, fence[lo]);
}
ret = max(ret, height * (hi - lo + 1));
}
return ret;
}
int main(void)
{
int cases;
cin >> cases;
assert(cases <= 50);
while(cases--)
{
int fenceNum;
cin >> fenceNum;
assert(fenceNum <= 20000 && fenceNum >= 1);
vector<int> fence(fenceNum);
for(int i = 0; i < fenceNum; i++)
{
cin >> fence[i];
assert(fence[i] <= 10000 && fence[i] >= 0);
}
cout << solve(0, fence.size()-1, fence) << endl;
}
return 0;
}3
7
7 1 5 9 6 7 3
20
7
1 4 4 4 4 1 1
16
4
1 8 2 2>> n개의 판자를 절반으로 나눠 두 개의 부분 문제를 만들면, 우리가 찾는 직사각형은 좌측, 우측, 가운데에 걸친 세 가지 유형이 있다.
>> case 1, 2를 나눠 각개격파하고 case 3으로 중간에 걸쳐지는 경우를 높이가 높은 쪽으로 확장하여 계산한다.
위 방법의 정당성 증명은 다음과 같이 귀류법으로 할 수 있다.

시간 복잡도 분석

예제3: 팬미팅 (문제 ID: FANMEETING, 난이도: 상)
https://www.algospot.com/judge/problem/read/FANMEETING
algospot.com :: FANMEETING
팬미팅 문제 정보 문제 가장 멤버가 많은 아이돌 그룹으로 기네스 북에 올라 있는 혼성 팝 그룹 하이퍼시니어가 데뷔 10주년 기념 팬 미팅을 개최했습니다. 팬 미팅의 한 순서로, 멤버들과 참가
www.algospot.com

>> 문제 해결의 아이디어 -> 카라츠바 알고리즘을 이용하여 답을 구할 수 있음
#include <iostream>
#include <vector>
#include <string>
using namespace std;
//num[]의 자릿수 올림 처리
void normalize(vector<int>& num)
{
num.push_back(0);
for (int i = 0; i < num.size(); i++)
{
if (num[i] < 0) //음수인 경우의 처리 -> 카라츠바 구현 후 이해 가능
{
int borrow = (abs(num[i]) + 9) / 10;
num[i+1] -= borrow;
num[i] += borrow * 10;
}
else
{
num[i+1] += num[i] / 10;
num[i] %= 10;
}
}
while(num.size() > 1 && num.back() == 0) num.pop_back();
}
vector<int> multiply(const vector<int>& a, const vector<int> b)
{
vector<int> c(a.size() + b.size() + 1, 0); //가능한 최대 자릿수
for(int i = 0; i < a.size(); i++)
for(int j = 0; j < b.size(); j++)
c[i+j] += a[i] * b[j];
normalize(c);
return c;
}
//a += b * (10^k);를 구현
void addTo(vector<int>& a, const vector<int>& b, int k) {
if(a.size() < b.size() + k)
a.resize(b.size() + k);
for(int i = 0; i < b.size(); i++) a[i+k] += b[i];
normalize(a);
}
//a -= b;를 구현 (a >= b 가정)
void subFrom(vector<int>& a, const vector<int>& b) {
for(int i = 0; i < b.size(); i++) a[i] -= b[i];
normalize(a);
}
vector<int> karatsuba(const vector<int>& a, const vector<int>& b) {
int an = a.size(), bn = b.size();
//a가 b보다 짧을 경우 둘을 바꾼다.
if(an < bn) {
return karatsuba(b, a);
}
//base case: a나 b가 비어있는 경우
if(an == 0 || bn == 0) {
return vector<int>();
}
//base case: a가 비교적 짧은 경우 O(n^2) 곱셈으로 변경한다.
if(an <= 50) {
return multiply(a, b);
}
int half = an / 2;
vector<int> a0(a.begin(), a.begin() + half); //a.begin() ~ (a.begin() + half - 1)
vector<int> a1(a.begin() + half, a.end()); //(a.begin() + half) ~ (a.end() -1) -> a.end(): 끝 요소 + 1
vector<int> b0(b.begin(), b.begin() + min<int>(b.size(), half));
vector<int> b1(b.begin() + min<int>(b.size(), half), b.end());
vector<int> z2 = karatsuba(a1, b1);
vector<int> z0 = karatsuba(a0, b0);
//a0 = a0 + a1; b0 = b0 + b1;
addTo(a0, a1, 0);
addTo(b0, b1, 0);
//z1 = (a0 + a1)(b0 + b1) - z0 - z2;
vector<int> z1 = karatsuba(a0, b0);
subFrom(z1, z0);
subFrom(z1, z2);
//ret = z0 + z1 * 10^half + z2 * 10^(half/2)
vector<int> ret;
addTo(ret, z0, 0);
addTo(ret, z1, half);
addTo(ret, z2, half + half);
return ret;
}
int hugs(const string& members, const string& fans)
{
int N = members.size(), M = fans.size();
vector<int> A(N), B(M); //N, M size 갖는 0으로 초기화
for(int i = 0; i < N; i++)
{
A[i] = (members[i] == 'M');
}
for(int i = 0; i < M; i++)
{
B[M-i-1] = (fans[i] == 'M');
}
vector<int> C = karatsuba(A, B);
int allHugs = 0;
for(int i = N-1; i < M; i++)
if(C[i] == 0)
allHugs++;
return allHugs;
}
int main(void)
{
int cases;
cin >> cases;
while(cases--) {
static char members[200001], fans[200001];
cin >> members >> fans;
cout << hugs(members, fans) << endl;
}
}4
FFFMMM
MMMFFF
1
FFFFF
FFFFFFFFFF
6
FFFFM
FFFFFMMMMF
2
MFMFMFFFMMMFMF
MMFFFFFMFFFMFFFFFFMFFFMFFFFMFMMFFFFFFF
2
시간 복잡도 분석
- 알고리즘의 수행 시간은 카라츠바 알고리즘과 같이 두 수의 곱셈에 좌우되므로, O(n^(lg3))
참고자료
- 구종만, < 프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략 >, 인사이트, 2012.11.01
- https://skyjwoo.tistory.com/entry/%EB%A1%9C%EA%B7%B8%EC%9D%98-%EC%84%B1%EC%A7%88-feat%EC%B9%B4%EB%9D%BC%EC%B8%A0%EB%B0%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98%EC%9D%98-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84
로그의 성질 (feat.카라츠바 알고리즘의 시간 복잡도)
곱셈 계산의 속도를 높이기 위해 고안된 카라츠바 알고리즘에 대해 보던 중 시간 복잡도를 구하는 과정에서 로그의 성질에 대해 정말 오랜만에 찾아보게 되었다. 카라츠바 알고리즘은 위키피디
skyjwoo.tistory.com
'Data Structure & Algorithm > 알고리즘 문제 해결 전략' 카테고리의 다른 글
| [알고리즘 문제 해결 전략] Chapter 20. 문자열 (0) | 2023.11.01 |
|---|---|
| [알고리즘 문제 해결 전략] Chapter 6. 무식하게 풀기 (1) | 2023.10.16 |
| [알고리즘 문제 해결 전략] ~Chapter 5 정리 (0) | 2023.10.05 |
| [알고리즘 문제 해결 전략] Chapter 1. 문제 해결 시작하기 (0) | 2023.10.01 |



