| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 지도학습
- OpenAI
- 오블완
- LG
- 회귀
- LG Aimers
- 머신러닝
- AI
- 티스토리챌린지
- GPT-4
- LG Aimers 4th
- 분류
- ChatGPT
- Machine Learning
- PCA
- supervised learning
- 딥러닝
- 해커톤
- LLM
- Classification
- deep learning
- regression
- gpt
Archives
- Today
- Total
SYDev
[데이터베이스] 7장. 릴레이션 정규화 본문
경희대학교 이영구 교수님의 데이터베이스 수업 복습용 게시물입니다.
릴레이션 정규화
- 부주의한 데이터베이스 설계 -> 제어할 수 없는 데이터 중복 야기 -> 여러 가지 갱신 이상(update anomaly) 유발
- 정규화(normalization): 릴레이션 스키마를 함수적 종속성과 기본 키를 기반으로 분석 -> 원래의 릴레이션을 분해 -> 중복과 세 가지 갱신 이상을 최소화
7.1. 정규화 개요
좋은 관계 데이터베이스 스키마를 설계하는 목적
- 정복의 중복과 갱신 이상 X
- 정보의 손실 X
- 실세계를 훌륭히 나타냄
- 애트리뷰트들 간의 관계가 잘 표현되는 것 보장
- 어떤 무결성 제약조건의 시행을 간단하게 함
- 효율성 측면도 고려
- first of all 갱신 이상 X -> secondly 효율성
갱신 이상(update anomaly)
수정 이상(modification anomaly)
- 반복된(중복된) 데이터 중에 일부만 수정하면, 데이터의 불일치가 발생
삽입 이상(insertion anomaly)
- 불필요한 정보를 함께 저장하지 않고는 어떤 정보를 저장하는 것이 불가능
삭제 이상(deletion anomaly)
- 유용한 정보를 함께 삭제하지 않고는 어떤 정보를 삭제하는 것이 불가능
정보의 중복
- 각 사원이 속한 부서 수만큼 동일한 사원의 tuple들이 존재 -> 사원이름, 사원 번호, 주소, 전화번호 등이 중복 -> 저장 공간 낭비


-> 정보의 중복
수정 이상(modification anomaly)
- 어떤 부서의 이름이 변경 -> 이 부서에 근무하는 일부 사원 tuple에서만 부서 이름 변경하면? -> 데이터베이스가 불일치 상태에 빠짐
삽입 이상(insertion anomaly)
- 신설된 부서 -> 사원이 한 명도 배정되지 않음 -> 이 부서에 관한 정보를 입력할 수 없음
삭제 이상(deletion anomaly)
- 어떤 부서에 속한 사원이 1명 -> 이 사원의 tuple 삭제 시 -> 해당 부서에 관한 정보도 릴레이션에서 삭제
->> 수정 이상, 삽입 이상, 삭제 이상을 총칭하여 갱신 이상(update anomaly)이라 함
릴레이션 분해
- 하나의 릴레이션을 두 개 이상의 릴레이션으로 나누는 것
- 필요한 경우 분해된 릴레이션들로부터 원래의 릴레이션을 다시 구할 수 있음을 보장한다는 원칙 기반
- 두 릴레이션으로부터 얻을 수 있는 정보 - 원래의 릴레이션 정보보다 적거나 많음 -> 잘못된 분해
- 함수적 종속성에 관한 지식 기반으로 함

-> 위 나쁜 설계 2의 릴레이션을 사원 릴레이션과 부서 릴레이션으로 나눔
부서 이름의 수정
- 어떤 부서에 근무하는 사원이 여러 명 있더라도 사원 1 릴레이션에는 부서 이름이 포함 X -> 수정 이상 X
새로운 부서를 삽입
- Although 신설 부서에 사원이 0명 -> 부서 릴레이션의 기본 키는 부서 번호 -> 이 부서에 관한 정보를 부서 릴레이션에 삽입 가능
마지막 사원 투플 삭제
- 유일한 사원 정보 삭제해도 -> 부서 정보는 부서 릴레이션에 남아 있음
정규형의 종류
- 제1 정규형
- 제2 정규형
- 제3 정규형
- BCNF(Boyce-Codd normal form)
- 제4 정규형
- 제5 정규형
- 일반적 산업계 데이터베이스 응용 -> BCNF까지만 고려
관계 데이터베이스 설계의 비공식적 지침
지침 1: 이해하기 쉽고 명확한 스키마
- 여러 엔티티 타입이나 관계 타입에 속한 attr들 -> 하나의 릴레이션에 포함 X

지침 2: 널값을 피하라
지침 3: 가짜 tuple이 생기지 않도록 하라
- 조인했을 때 생기는 원래 없었던 tuple
지침 4: 스키마를 정제하라
7.2. 함수적 종속성
함수적 종속성의 개요
- 릴레이션의 애트리뷰트들의 의미로부터 결정됨
- 릴레이션 스키마에 대한 주장, 특정 인스턴스에 대한 주장 X
- 가능한 모든 인스턴스들이 만족해야 함
- 제2 정규형 ~ BCNF까지 적용됨
결정자(determinant)
- 어떤 애트리뷰트의 값 -> 다른 애트리뷰트의 값을 고유하게 결정
- 결정자: 주어진 릴레이션에서 다른 애트리뷰트(또는 애트리뷰트들의 집합)를 고유하게 결정하는 하나 이상의 애트리뷰트
- A -> B: A가 B를 결정한다(A는 B의 결정자이다.)

- 사원번호 -> 사원이름, 주소, 전화번호
- 부서번호 -> 부서이름
- f(사원번호, 부서번호) -> 직책
- f(사원번호) -X> 직책
함수적 종속성
- attribute A가 attribute B의 결정자 -> B가 A에 함수적으로 종속
- 애트리뷰트 B가 애트리뷰트 A에 함수적으로 종속하는 필요 충분 조건 -> 각 A값에 대해 반드시 한 개의 B값이 대응
완전 함수적 종속성(FFD: Full Functional Dependency)
- 애트리뷰트 B가 A에 함수적 종속 + 애트리뷰트 A의 어떠한 진부분 집합에도 함수적으로 종속 X -> 애트리뷰트 B가 애트리뷰트 A에 완전하게 함수적으로 종속
- A의 진부분 집합 A' -X> B

이행적 함수적 종속성(transitive FD)
- 애트리뷰트 A, B, C에 대하여, 애트리뷰트 C가 이행적으로 A에 종속한다는 필요 충분 조건

7.3. 릴레이션 분해
- 중복이 감소되고 갱신 이상이 줄어드는 장점 but 몇 가지 문제점
- 조인이 필요 없는 질의가 -> 분해 후 -> 조인을 필요로 하는 질의로 바뀔 수 있음
- 분해된 릴레이션들로 원래 릴레이션 재구성이 되지 않을 수도 있음
무손실 분해(lossless decomposition)
- 분해된 두 릴레이션 조인 -> 원래의 릴레이션에 들어 있는 정보를 완전하게 얻을 수 있음
- 정보의 손실 -> 분해된 릴레이션을 다시 조인한 결과가 원래 릴레이션보다 정보가 적거나 많은 경우 모두 포함
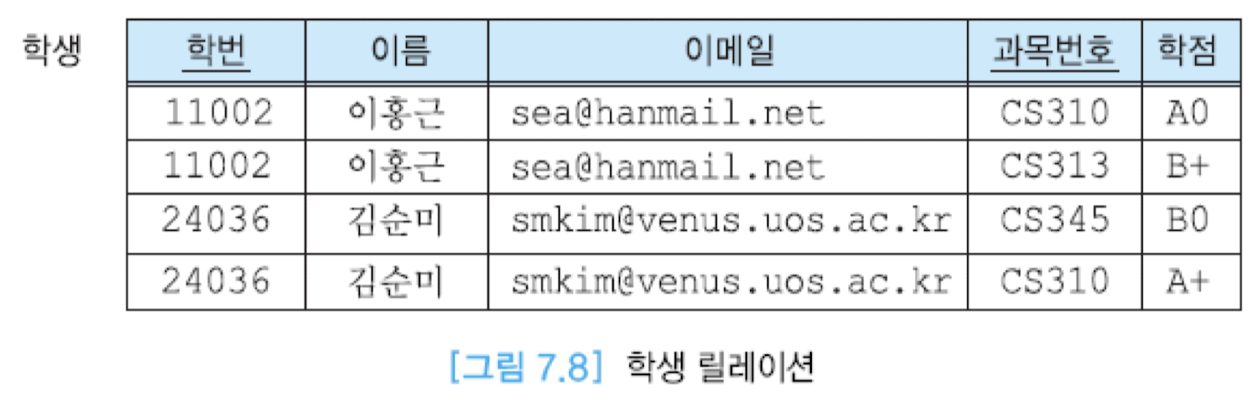
학번 -> 이름, 이메일
이메일 -> 학번, 이름
(학번, 과목번호) -> 학점


-> 좌측은 무손실 분해. 학번을 기준으로 조인하면 튜플이 4개로 동일
-> 우측은 불필요한 분해. 굳이 나눠서 테이블 개수만 늘어남
-> 학번과 과목 번호가 합쳐진 것이 키 -> 이런 키 정보를 모두 포함하지 않고 분해 -> 손실 발생

->가짜 튜플 발생
7.4. 제1 정규형, 제2 정규형, 제3 정규형, BCNF
제1 정규형
- 릴레이션의 모든 애트리뷰트에 반복 그룹(repeating group)이 나타나지 않으면 제 1정규형 만족

-> 제1 정규형 만족 X

-> 제1 정규형 만족
제1 정규형에 존재하는 갱신 이상

- 두 번째 튜플의 학과 이름을 인공지능으로 변경 -> 수정 이상 발생 -> 전화번호가 같은 학과는 모두 이름을 변경해줘야 데이터베이스 일관성 유지
- 엔티티 무결성 제약 조건에 따라 기본 키에 널값 X -> 1명도 속하지 않는 학과에 속하는 학생의 튜플은 삽입 불가능 -> 삽입 이상
- 학과의 마지막 학생 1명의 정보 삭제 -> 해당 학과 정보도 삭제 -> 삭제 이상
갱신 이상 발생 이유
- 기본 키에 대한 부분 함수적 종속성이 존재
- 두 개의 엔티티가 같은 테이블에 존재 -> 이를 분해한 것이 제2 정규형
제2 정규형
- 제1 정규형 만족(중복 애트리뷰트 X) + 모든 애트리뷰트들이 기본 키에 완전하게 함수적으로 종속
- 기본 키가 두 개 이상의 애트리뷰트로 구성 -> 제1 정규형이 제2 정규형 만족하는가 고려
- prime attribute: 어떤 후보 키(튜플을 유일하게 식별가능하게 함)에 속한 attr
- non-prime attribute: 어떤 후보 키에도 속하지 않는 attr -> non-prime attr은 완전하게 함수적으로 종속해야 함
- 기본 키가 하나면 부분함수적 종속성 X -> 기본 키가 하나의 attr -> 제2 정규형 만족
제2 정규형에 존재하는 갱신 이상

- 수정 이상
- 삽입 이상
- 삭제 이상
갱신 이상이 생기는 이유
- 이행적 함수적 종속성이 존재하기 때문
제3 정규형
- 제2 정규형 만족(중복 애트리뷰트 X, 부분 함수적 종속성 X) + 키가 아닌 모든 애트리뷰트가 기본 키에 이행적으로 종속 X

제3 정규형에 존재하는 갱신 이상
- 기본 키인 (학번, 과목)에 (학번, 과목) -> 강사 가 성립 -> 제3정규형 만족

- 수정 이상
- 삽입 이상
- 삭제 이상
갱신 이상 발생 이유
- 키가 아닌 애트리뷰트(강사)가 다른 애트리뷰트를 결정하기 때문
- 이 릴레이션의 후보 키는 (학번, 과목)과 (학번, 강사)
BCNF
- 제3 정규형 만족(중복 attr X, 부분함수적 종속성 X, 이행적 종속성 X) + 모든 결정자가 후보 키
- 하나의 후보 키 릴레이션이 제3 정규형 만족 -> BCNF도 만족

-> BCNF 만족 X

-> BCNF로 분해
7.5. 역정규화(denormalization)
정규화 장점
- 정규화 단계 진행될수록 -> 중복 감소, 갱신 이상 감소
- 무결성 제약조건을 시행하기 위해 필요한 코드 양도 감소
정규화 단점
- 다음 정규형으로 진행될 때마다 하나의 릴레이션이 최소 2개로 분해 -> 분해되기 전 릴레이션 대상으로 조인이 필요 없지만, 분해된 릴레이션을 대상으로 질의를 할 때 -> 같은 정보를 얻기 위해서 보다 많은 릴레이션을 접근해야 함 -> 조인의 필요성 증가

-> 하나의 릴레이션일 때는 조인 필요 X
-> 두 개의 릴레이션으로 나눠지면 조인 필요
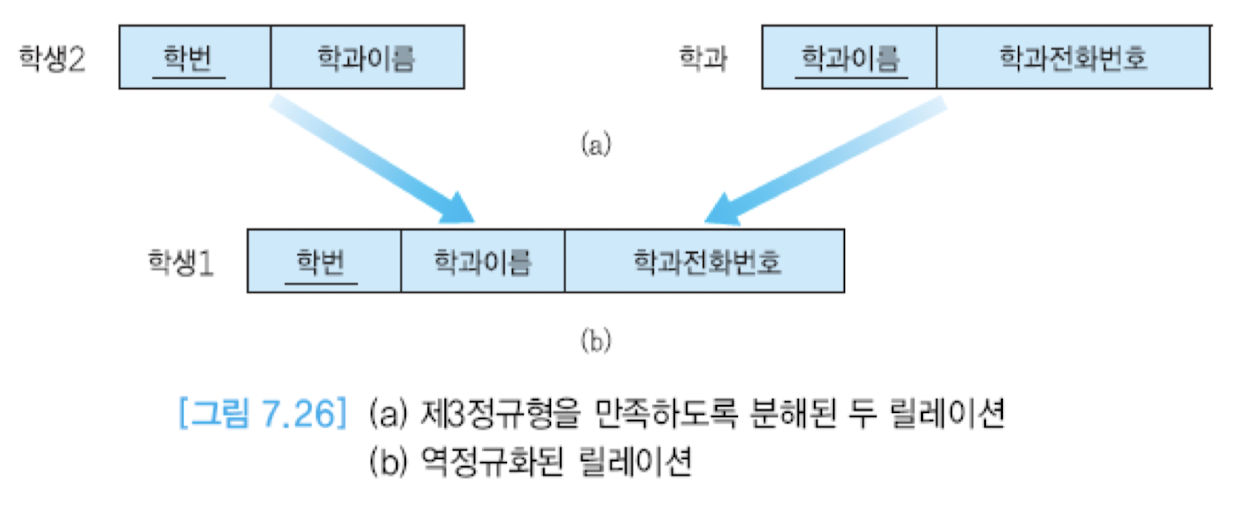
역정규화
- 역정규화 -> 데이터 중복 및 갱신 이상을 대가로 성능상의 요구 만족
- 두 개 이상의 릴레이션을 합쳐서 -> 하나의 릴레이션으로 만드는 작업
- 보다 낮은 정규형으로 되돌아가는 것
728x90
반응형
'3학년 1학기 전공 > 데이터베이스' 카테고리의 다른 글
| [데이터베이스] 9장. 트랜잭션 (0) | 2024.06.18 |
|---|---|
| [데이터베이스] 10장. 데이터베이스 보안과 권한 관리 (0) | 2024.05.31 |
| [데이터베이스] 8장. 뷰와 시스템 카탈로그 (0) | 2024.05.23 |
| [데이터베이스] 5.2. ER 모델 (1) | 2024.05.03 |
| [데이터베이스] 5.1. 데이터베이스 설계의 개요 (0) | 2024.05.02 |




