| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 오블완
- PCA
- LG
- 머신러닝
- OpenAI
- 티스토리챌린지
- Classification
- 지도학습
- 회귀
- Machine Learning
- 딥러닝
- 해커톤
- gpt
- LG Aimers
- LG Aimers 4th
- deep learning
- ChatGPT
- LLM
- supervised learning
- 분류
- GPT-4
- AI
- regression
Archives
- Today
- Total
SYDev
[알고리즘] Chapter 2. 분할정복법(Divide-and-Conquer) 본문
경희대학교 한치근 교수님의 알고리즘 수업을 기반으로 정리한 글입니다.
분할정복(Divide-and-Conquer)식 설계 전략
- 분할(Divide): 해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나눔
- 정복(Conquer): 나눈 작은 문제를 각각 해결
- 통합(Combine): (필요하다면) 해결된 해답을 모음
-> 이런 문제 해결 방법을 하향식(top-down) 접근방법이라 함
1. 이분검색(binary search): 재귀식 방식
- 설계 전략
- x가 배열의 중간에 위치한 항목과 같으면 stop, 그렇지 않으면
- Divide: 배열을 반으로 나누어 x와 중앙값을 비교하여 배열 반쪽을 선택
- Conquer: 선택된 반쪽 배열에서 x를 찾음
- x가 배열의 중간에 위치한 항목과 같으면 stop, 그렇지 않으면
def bs(data, item, low, high):
# item 존재 X
if(low > high):
return -1
mid = (low + high) // 2
# 탐색 성공
if(item == data[mid]):
return mid
# 우측 배열
elif(item > data[mid]):
return bs(data, item, mid + 1, high)
# 좌측 배열
else:
return bs(data, item, low, mid - 1)
data = [1, 3, 5, 6, 7, 9, 10, 13, 17, 19]
n = 10
location = bs(data, 17, 0, n - 1)
print(location)- 시간복잡도


2. 합병정렬(mergesort)
- Mergesort
- 문제: n개의 정수를 비내림차순으로 정렬
- 입력: 정수 n, 크기가 n인 배열 S[1..n]
- 출력: 비내림차순으로 정렬된 배열 S[1..n]
- 보기: 27, 10, 12, 20, 25, 13, 15, 22

- 배열 S를 U와 V로 분할
- U와 V에 대해서 mergesort 호출
- U와 V에 대해서 merge 호출
- Merge
- 문제: 두 개의 정렬된 배열을 하나의 정렬된 배열로 합병하시오.
- 입력: (1) 양의 정수 h, m, (2) 정렬된 배열 U[1..h], V[1..m]
- 출력: U와 V에 있는 키들을 하나의 배열에 정렬한 S[1..h+m]
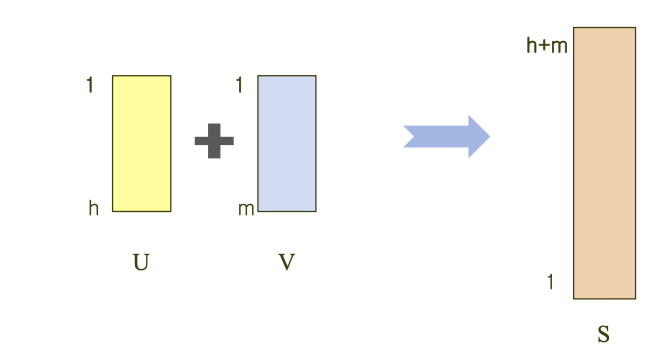


- U, V의 iterator i, j를 선언, i, j를 모두 추적하는 k를 선언
- 크기에 따라 i, j를 ++ -> k++
- i가 모두 돌았으면, j부터 m까지(나머지 부분)를 S에 copy | j가 모두 돌았으면 i부터 h까지를 S에 copy
- 시간복잡도
- 단위연산: U[i]와 V[j]의 비교
- 입력크기: 2개의 입력 배열에 들어 있는 항목의 개수: h&m
- i = h + 1, j = m인 상태로 loop에서 빠져나가는 경우
- ex) U: 4 5 6 7, V: 1 2 3 8
- W(h, m) = h + m - 1
- 단위연산: 합병 알고리즘 merge에서 발생하는 비교
- 입력크기: 배열 S에 들어 있는 항목의 개수 n
- W(h, m) = W(h) + W(m) + h + m - 1
- W(n) = 2W(n/2) + n - 1, W(1) = 0
- W(n) ∈ Θ(nlgn) -> 도사정리 적용

- 공간복잡도
- 제자리정렬(in-place sort) 알고리즘: 추가적인 저장장소를 사용하지 않고 정렬하는 알고리즘
- mergesort는 제자리 정렬이 X

- 총 저장 장소의 크기: n + n/2 + n/4 + ... = 2n
- 2n ∈ Θ(n)
def mergeSort(n, s):
mid = n // 2
u = s[:mid]
v = s[mid:]
h = len(u)
m = len(v)
if(n > 1):
mergeSort(h, u)
mergeSort(m, v)
merge(h, m, u, v, s)
def merge(h, m, u, v, s):
i = j = k = 0
while(i < h and j < m):
if(u[i] < v[j]):
s[k] = u[i]
i += 1
else:
s[k] = v[j]
j += 1
k += 1
if(i >= h):
remained = v[j:m]
for value in remained:
s[k] = value
k += 1
else:
remained = u[i:h]
for value in remained:
s[k] = value
k += 1- 공간복잡도가 향상된 알고리즘
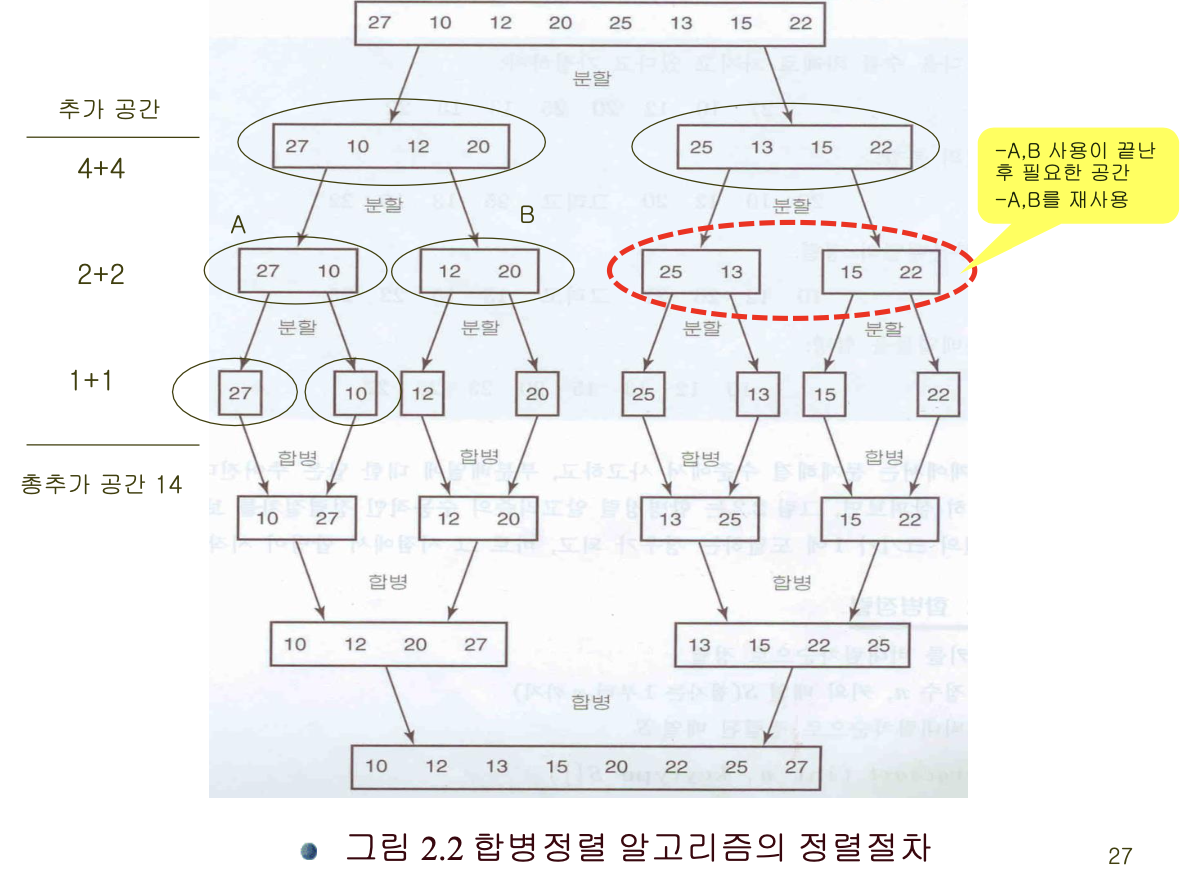
-> 공간 재사용

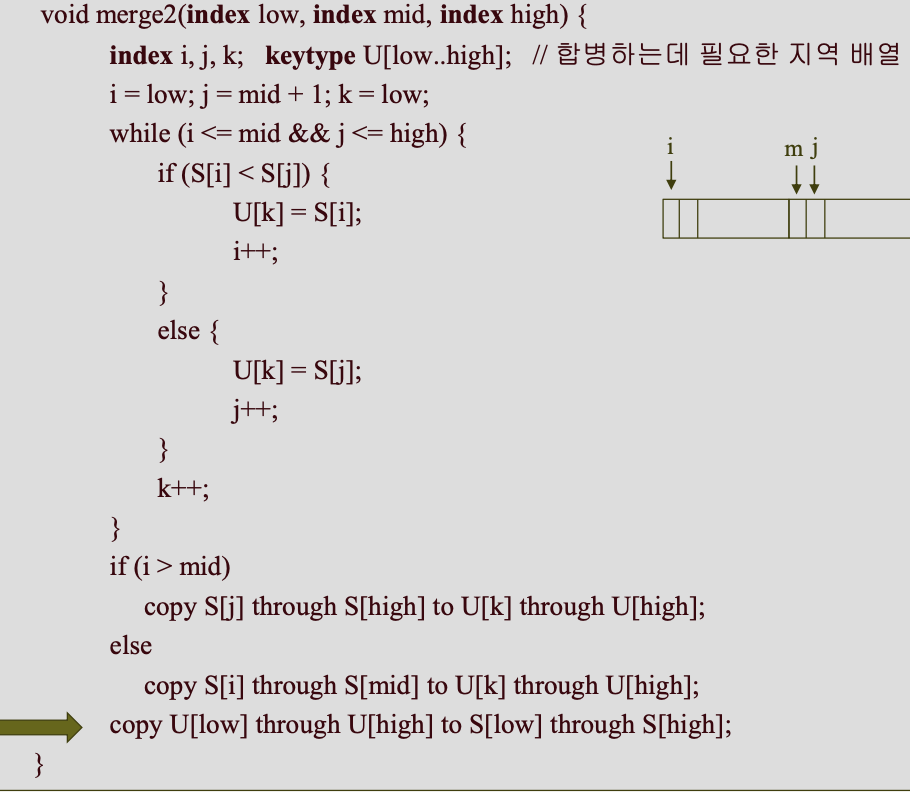
-> 반으로 나눠진 S의 정렬된 형태를 U에 저장하다가, 마지막에 S로 최종 결과물을 복사


def mergeSort2(s, low, high):
if(low < high):
mid = (low + high) // 2
mergeSort2(s, low, mid)
mergeSort2(s, mid + 1, high)
merge2(s, low, mid, high)
def merge2(s, low, mid, high):
u = [0 for i in range(high - low + 1)]
i = low
j = mid + 1
k = 0
while(i <= mid and j <= high):
if(s[i] < s[j]):
u[k] = s[i]
i += 1
else:
u[k] = s[j]
j += 1
k += 1
if(i > mid):
remained = s[j:high+1]
for value in remained:
u[k] = value
k += 1
else:
remained = s[i:mid+1]
for value in remained:
u[k] = value
k += 1
for i in range(len(u)):
s[low + i] = u[i]
-> index 유의하여 구현
3. 빠른정렬(Quicksort)
- 분할 교환 정렬(partition exchange sort)
- 문제: n개의 정수를 비내림차순으로 정렬
- 입력: 정수 n>0, 크기가 n인 배열S[1..n]
- 출력: 비내림차순으로 정렬된 배열 S[1..n]
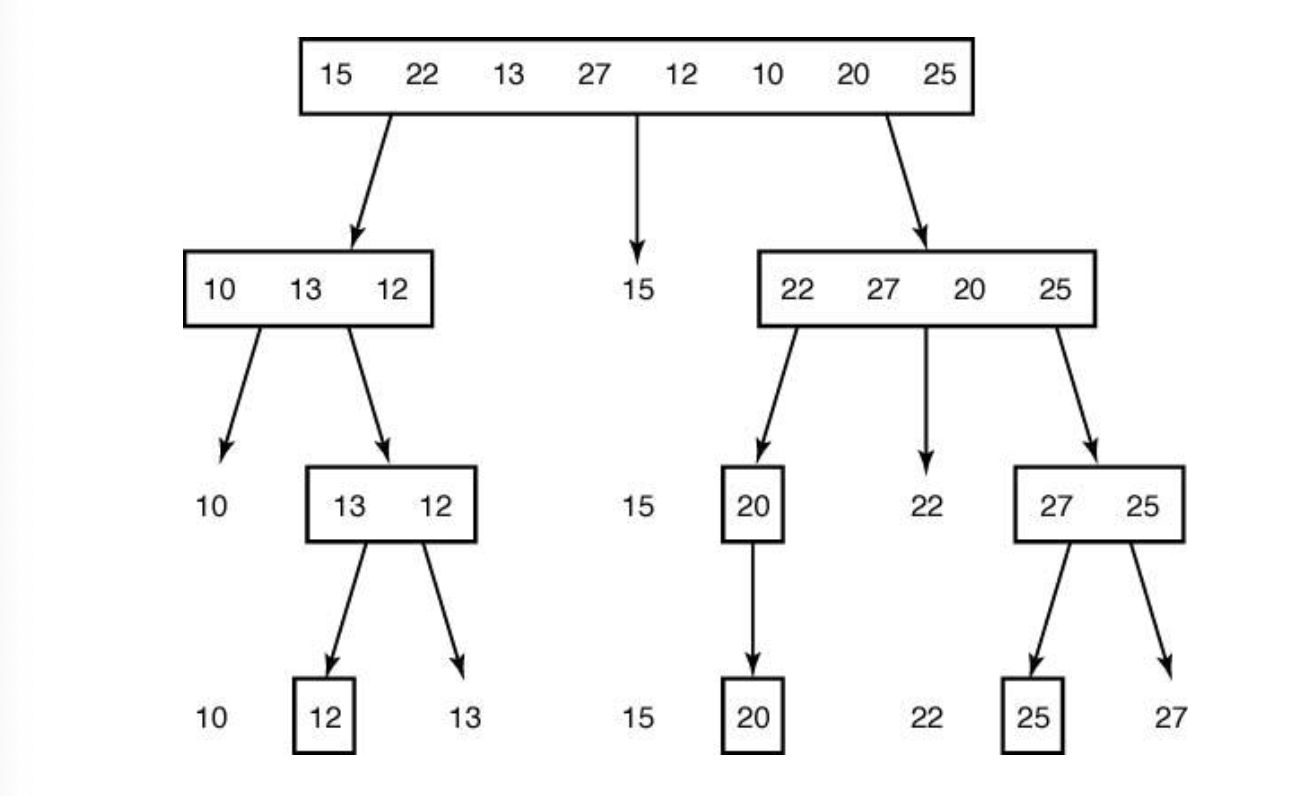
- quicksort

- partition 수행한 값을 pivotpoint에 할당
- quicksort(low, pivotpoint - 1)
- quicksort(pivotpoint + 1, high)
- partition

- pivotitem으로 첫 번째 항목 선택
- i = pivotitem + 1, i번째 item이 pivotitem보다 작으면 j번째 항목과 i번째 항목 위치 변경, 이후 j++ -> j 왼쪽의 아이템들은 모두 pivotitem보다 작은 items
- pivotpoint = j & pivotitem을 pivotpoint에 위치
def exchange(index1, index2, s):
temp = s[index1]
s[index1] = s[index2]
s[index2] = temp
def partition(s, low, high):
pivotItem = s[low]
j = low
for i in range(low + 1, high + 1):
if(s[i] < pivotItem):
j += 1
exchange(i, j, s)
pivotPoint = j
exchange(low, pivotPoint, s)
return pivotPoint
def quickSort(s, low, high):
if(low < high):
pivotPoint = partition(s, low, high)
quickSort(s, low, pivotPoint - 1)
quickSort(s, pivotPoint + 1, high)
s = [3, 5, 2, 9, 10, 14, 4, 8]
quickSort(s, 0, 7)
print(s)
- partition 시간복잡도
- 단위연산: S[i]와 pivotitem 비교
- 입력크기: 부분배열이 가지고 있는 항목의 수, n = high - low + 1
- 분석: 배열의 첫 번째 항목만 제외하고 모든 항목을 한 번씩 비교하므로, T(n) = n - 1
- quicksort 분석
- 단위연산: partition의 S[i]와 pivotitem 비교
- 입력크기: 배열 S가 가지고 있는 항목의 수, n
- 분석: 입력이 비내림차순으로 정렬된 경우가 최악, pivotitem보다 작은 항목이 없으므로,
- 피벗 아이템의 좌측: 크기가 0인 배열
- 피벗 아이템의 우측: 크기가 n-1인 배열
- T(n) = T(0) + T(n - 1) + n - 1, T(0) = 0

-> W(n) ∈ Θ(n^2)
+ A(n) ∈ Θ(nlgn)
+ B(n) ∈ Θ(nlgn)
4. 행렬 곱셈(matrix multiplication)
- 문제: n x n 크기의 행렬의 곱을 구하시오
- 입력: 양수 n, n x n 크기의 행렬 A와 B
- 출력: 행렬 A와 B의 곱인 C

- 시간복잡도
- 단위연산: 가장 안쪽의 루프에 있는 곱셈하는 연산
- 입력크기: 행과 열의 수, n
- Every case: 총 곱셈의 횟수
- T(n) = n * n * n = n^3 ∈ Θ(n^3)

-> 한 단계 당 8번의 곱셈 연산 필요
- 개선된 알고리즘 시간복잡도
- 단위연산: 가장 안쪽의 루프에 있는 덧셈하는 연산
- 입력크기: 행과 열의 수, n
- Every case: 총 덧셈의 횟수
- T(n) = (n - 1) * n * n = n^3 - n^2 ∈ Θ(n^3)
- Strassen algorithm
- n이 2의 거듭제곱이고, 각 행렬을 4개의 submatrix로 나눈다고 가정. 두 n x n 행렬 A와 B의 곱 C
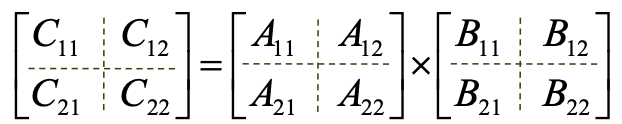
- Strassen의 해

- 문제: n이 2의 거듭제곱일 때, n x n 크기의 두 행렬의 곱을 구하시오.
- 입력: 정수 n, n x n 크기의 행렬 A와 B
- 출력: 행렬 A와 B의 곱인 C

- A, B를 4개의 부분 행렬로 분할
- Strassen 방법을 사용하여 C = A * B 계산 - strassen(n/2, A11 + A22, B11 + B22, M1)
- 임계점에서 단순 알고리즘 계산
from numpy import *
def strassen(n, A, B, C):
threshold = 2
A11 = array([[A[rows][cols] for cols in range(int(n/2))]for rows in range(int(n/2))])
A12 = array([[A[rows][cols] for cols in range(int(n/2), n)]for rows in range(int(n/2))])
A21 = array([[A[rows][cols] for cols in range(int(n/2))]for rows in range(int(n/2), n)])
A22 = array([[A[rows][cols] for cols in range(int(n/2), n)]for rows in range(int(n/2), n)])
B11 = array([[B[rows][cols] for cols in range(int(n/2))]for rows in range(int(n/2))])
B12 = array([[B[rows][cols] for cols in range(int(n/2), n)]for rows in range(int(n/2))])
B21 = array([[B[rows][cols] for cols in range(int(n/2))]for rows in range(int(n/2), n)])
B22 = array([[B[rows][cols] for cols in range(int(n/2), n)]for rows in range(int(n/2), n)])
if(n <= threshold):
C = array(A) @ array(B)
else:
M1 = M2 = M3 = M4 = M5 = M6 = M7 = array([])
M1 = strassen(int(n/2), (A11 + A22) , (B11 + B22), M1)
M2 = strassen(int(n/2), (A21 + A22) , B11, M2)
M3 = strassen(int(n/2), A11 , (B12 - B22), M3)
M4 = strassen(int(n/2), A22 , (B21 - B11), M4)
M5 = strassen(int(n/2), (A11 + A12) , B22, M5)
M6 = strassen(int(n/2), (A21 - A11) , (B11 + B12), M6)
M7 = strassen(int(n/2), (A12 - A22) , (B21 + B22), M7)
C = vstack([ hstack([M1 + M4 - M5 + M7, M3 + M5]), hstack([M2 + M4, M1 + M3 - M2 + M6]) ])
return C
n = 4
A=[ [1,2,0,2], [3,1,0,0], [0,1,1,2],[2,0,2,0]]
B=[ [0,3,0,2], [1,1,4,0], [1,1,0,2],[0,5,2,0]]
C = array(A)@array(B)
D = [[0 for cols in range(n)]for rows in range(n)]
print(C)
D=strassen(n, A, B, D)
print(D)
- Strassen 알고리즘 시간복잡도
- 단위연산: 곱셈 연산
- 입력크기: 행과 열의 수, n
- Every case:
- T(n) = 7T(n/2), T(1) = 1

-> strassen에서는 곱셈이 7번!!
- Strassen 알고리즘 시간복잡도 2
- 단위연산: 덧셈/뺄셈 연산
- 입력크기: 행과 열의 수, n
- Every case:
- T(n) = 7T(n/2) + 18(n/2)^2 , T(1) = 0 -> 7회의 곱셈과 18회의 덧셈


- Discussion

5. 큰 정수 계산법
- 문제: 2개의 큰 정수 u와 v를 곱하라
- 입력: 큰 정수 u와 v, 크기 n
- 출력: prod(u와 v의 곱)
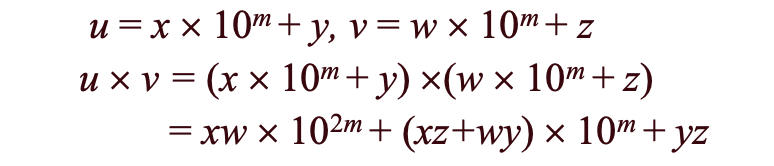
-> 2개의 큰 정수 곱셈을 4개의 작은 정수 곱셈으로 변환 가능

- 개선된 방법(Karatsuba)

- ex) a = a1 * 10 + a0, b = b1 * 10 + b0
- 기존 방식: a * b = (a1 * 10 + a0)(b1 * 10 + b0)
- a1b1, a1b0, a0b1, a0b0
- 카라츠바
- z0 = a0 * b0
- z2 = a1 * b1
- z1 = (a0 + a1) * (b0 + b1) - z0 - z2
- -> 곱셈이 4번에서 3번으로 줄어듦
- 기존 방식: a * b = (a1 * 10 + a0)(b1 * 10 + b0)

- 시간복잡도
- 기존: W(n) ∈Θ(n^lg4) = Θ(n^2)
- 카라츠바: W(n)∈Θ(n^lg3) ~= Θ(n^1.58)
6. 임계값결정
- 어느 크기의 문제가 딜 때까지 분할할 것인가
- optimal threshold value를 결정하는 방법

- 분할정복을 사용하지 말아야 하는 경우
- 크기가 n인 입력이 2개 이상의 조각으로 분할되며, 분할된 부분들의 크기가 거의 n에 가깝게 되는 경우 -> exponential
- ex) T(n) = 2T(n - 1) + n
- 크기가 n인 입력이 거의 n개 조각으로 분할되며, 분할된 부분의 크기가 n/c인 경우. 여기서 c는 상수 -> Θ(n^lgn)
- ex) T(n) = nT(n/2) + n
7. 도사 정리(The Master Theorem)
- 1보다 큰 상수 a, b, 어떤 함수 f(n), 음이 아닌 정수 n에 대해서 정의된 재현식 T(n)이 다음 형태라 가정
- T(n) = a x T(n/b) + f(n)
- T(n)은 다음과 같은 점근적 한계점(asymptotic bound)을 가질 수 있음



728x90
반응형
'4학년 1학기 전공 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Chapter 3. 동적계획(Dynamic Programming) (0) | 2025.04.21 |
|---|---|
| [알고리즘] Chapter 1. 알고리즘: 효율, 분석 그리고 차수 (1) | 2025.04.14 |


