| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- LG
- GPT-4
- AI
- ChatGPT
- deep learning
- 머신러닝
- regression
- 회귀
- 오블완
- 지도학습
- 분류
- LLM
- 딥러닝
- supervised learning
- 해커톤
- LG Aimers 4th
- OpenAI
- 티스토리챌린지
- PCA
- Classification
- gpt
- Machine Learning
- LG Aimers
Archives
- Today
- Total
SYDev
Chapter 04-2: 확률적 경사 하강법 본문
클래스 SGDClassifier를 이용하여 파이썬으로 확률적 경사 하강법 모델을 구현해보자.
손실 함수와 경사 하강법에 대한 자세한 설명은 내용이 길어 따로 포스팅했다!
>> https://sypdevlog.tistory.com/116
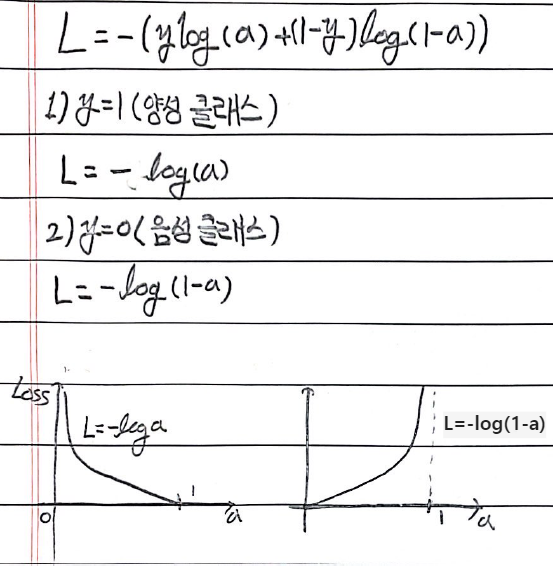
로지스틱 손실 함수
y를 타깃, a를 로지스틱 함수의 결과값이라고 했을 때, 손실 함수는 다음과 같이 y가 1일 때, y가 0일 때로 구분할 수 있다.
SGDClassifier
#데이터프레임 넘파이로 변환
import pandas as pd
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
#훈련, 테스트 데이터셋 스플릿
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target =train_test_split(fish_input, fish_target, random_state=42)
#데이터 전처리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
#확률적 경사 하강법 모델 훈련
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
0.773109243697479
0.775
sc.partial_fit(train_scaled, train_target) #epoch를 한 번 더 실행하여 정확도 보완
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
0.8151260504201681
0.85-> 에포크 횟수를 늘릴수록 정확도는 좋아지지만, 과대적합의 확률도 up
import numpy as np
sc = SGDClassifier(loss='log', random_state=42)
train_score=[]
test_score=[]
classes = np.unique(train_target)
#epoch를 300회 반복
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
import matplotlib.pyplot as plt
plt.plot(train_score) #파랑선
plt.plot(test_score) #주황선
plt.axvline(105, 0, 1, linestyle='--')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
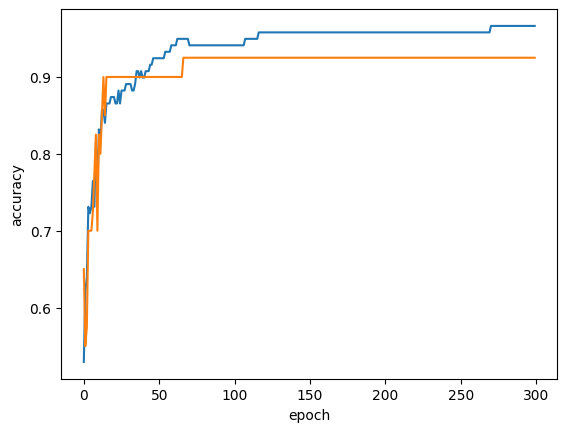
-> epoch가 105를 넘어갈때쯤부터 훈련 세트와 테스트 세트의 차이가 벌어지고 있으므로, 105 이후부터는 과대적합이 발생한다고 판단하고 학습을 종료한다. >> 조기 종료(early stopping)!!
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42) #loss 매개변수의 기본값은 hinge!
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
0.957983193277311
0.925
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
0.9495798319327731
0.925
참고자료
- 박해선, <혼자 공부하는 머신러닝+딥러닝>, 한빛미디어(주), 2022.2.4
- https://plan0a-0z-entering-security.tistory.com/110
[Do it] 로지스틱 회귀, 시그모이드 함수, 로지스틱 손실 함수
04-1 | 초기 인공지능 알고리즘과 로지스틱 회귀를 알아봅니다 . #1. 퍼셉트론 1957년 이진 분류 문제에서 최적의 가중치를 학습하는 퍼셉트론 알고리즘 발표 * 이진 분류 : 임의의 샘플 데이터를 Tru
plan0a-0z-entering-security.tistory.com
로지스틱 회귀 (Logistic Regression)
로지스틱 회귀
velog.io
15. Matplotlib 수평선/수직선 표시하기
 그래프의 특정 위치에 수직선/수평선을 표시하기 위해서 **mat…
wikidocs.net
728x90
반응형
'KHUDA 4th > 머신러닝 기초 세션' 카테고리의 다른 글
| Chapter 05-1: 결정 트리 (0) | 2023.08.22 |
|---|---|
| [KHUDA 4th] 머신러닝 3주차 기초 세션 (08.16) (1) | 2023.08.19 |
| 경사 하강법 (0) | 2023.08.13 |
| Chapter 04-1: 로지스틱 회귀 (1) | 2023.08.13 |
| [KHUDA 4th] 머신러닝 2주차 기초 세션 (08.10) (1) | 2023.08.10 |




