Chapter 04-1: 로지스틱 회귀

로지스틱 회귀 알고리즘을 이용해 다중 분류 문제를 해결해보자. 

 

 

다중 분류(multi-class classification)

• 다중 분류: 타깃 데이터에 2개 이상의 클래스가 포함된 분류 문제를 의미한다.

 

로지스틱 회귀(logistic regression)

• 로지스틱 회귀: 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1사이의 값으로 예측해주고, 그 확률에 따라 해당 데이터가 속하는 범주를 분류해주는 알고리즘이다. -> 회귀를 사용하긴 하지만 결국엔 분류 알고리즘!

 

선형 회귀와 로지스틱 회귀의 구조

 

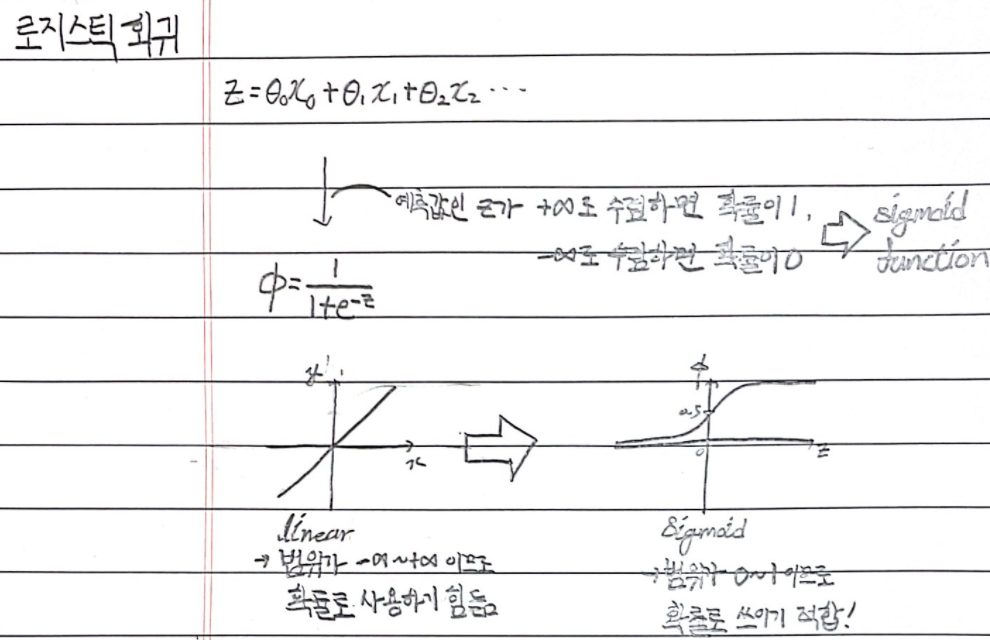
 위 그림과 같이 선형 회귀의 경우에는 예측값을 그대로 확률로 사용하기에 무리가 있다.

->> 선형 방정식을 학습한 z값을 구해서, 이를 시그모이드 함수에 대입해 0~1 사이의 확률을 얻는다.

 

로지스틱 회귀의 hyper parameter C

• 로지스틱 회귀의 비용함수는 아래의 형태를 가진다
• Λ는 로지스틱 회귀의 hyper parameter인데, 로지스틱 회귀 모델에서는 이의 역수인 C를 조정한다.

출처: https://dnai-deny.tistory.com/9

 

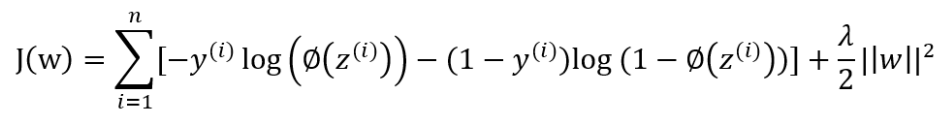
로지스틱 회귀의 penalty 매개변수

• LogisticRegression의 매개변수 penalty는 L1규제와 L2규제를 선택할 수 있고, L2규제가 디폴트이다.
• L1규제는 도움이 되지 않는 계수를 0으로 학습하도록 유도하기 때문에, 중복되지 않는 최소한의 유용한 features 를 선택할 때 사용된다.

 

 

소프트맥스 함수

• 소프트 맥스 함수는 클래스가 여러 개 존재할 때, 각각의 클래스의 z값을 확률로 변환하는 함수이다.
• 클래스가 7개 있을 때, 각각의 확률은 다음과 같이 계산한다.

e_sum = e^(z1) + e^(z2) +....+e^(z7)

s1 = e^(z1) / e_sum, s2 = e^(z2) / e_sum, ... , s7 = e^(z7) / e_sum

 

 

로지스틱 회귀를 이용한 다중 분류의 해결

KNN을 이용한 확률 예측

• 위에서는 로지스틱 회귀를 이용해 각 샘플이 클래스에 속할 확률을 구할 수 있다고 언급했는데, 그 이전에 KNN을 이용해 확률을 구해보자.

import pandas as pd

fish = pd.read_csv('https://bit.ly/fish_csv_data')

fish.head() #처음 5개 행 출력

 

 

출력 결과

 

print(pd.unique(fish['Species'])) #중복되는 구성원은 지우고 하나씩만 남김

['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']

 

fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()

fish_target = fish['Species'].to_numpy()

""" 훈련, 테스트 세트 스플릿 """

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target =train_test_split(fish_input, fish_target, random_state=42)

""" 데이터셋 정규화 """

from sklearn.preprocessing import StandardScaler

ss = StandardScaler()

ss.fit(train_input)

train_scaled = ss.transform(train_input)

test_scaled = ss.transform(test_input)

""" KNN 모델 학습 """

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier(n_neighbors=3)

kn.fit(train_scaled, train_target)

print(kn.score(train_scaled, train_target))

print(kn.score(test_scaled, test_target))

0.8907563025210085
0.85

 

print(kn.predict(test_scaled[:5]))

 

import numpy as np

proba = kn.predict_proba(test_scaled[:5]) #클래스별 확률값 반환

print(np.round(proba, decimals=4)) #소수점 네 번째 자리까지 표기

['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
[[0.     0.     1.     0.     0.     0.     0.    ]
 [0.     0.     0.     0.     0.     1.     0.    ]
 [0.     0.     0.     1.     0.     0.     0.    ]
 [0.     0.     0.6667 0.     0.3333 0.     0.    ]
 [0.     0.     0.6667 0.     0.3333 0.     0.    ]]

-> 표기 가능한 확률은 0, 0.3333, 0.6667, 1이 전부이므로 정확하지 못하다.

 

+ 그렇다면 k값을 바꿔보면 어떻게 될까?

kn = KNeighborsClassifier(n_neighbors=9)

kn.fit(train_scaled, train_target)

print(kn.score(train_scaled, train_target))

print(kn.score(test_scaled, test_target))

print(kn.predict(test_scaled[:5]))

proba = kn.predict_proba(test_scaled[:5])

print(np.round(proba, decimals=4))

0.7983193277310925
0.825
['Perch' 'Smelt' 'Perch' 'Perch' 'Perch']
[[0.     0.     0.6667 0.     0.3333 0.     0.    ]
 [0.     0.     0.1111 0.     0.     0.8889 0.    ]
 [0.     0.     0.5556 0.4444 0.     0.     0.    ]
 [0.     0.     0.5556 0.     0.3333 0.     0.1111]
 [0.     0.     0.8889 0.     0.1111 0.     0.    ]]

 

kn = KNeighborsClassifier(n_neighbors=20)

kn.fit(train_scaled, train_target)

print(kn.score(train_scaled, train_target))

print(kn.score(test_scaled, test_target))

print(kn.predict(test_scaled[:5]))

proba = kn.predict_proba(test_scaled[:5])

print(np.round(proba, decimals=4))

0.6470588235294118
0.725
['Perch' 'Smelt' 'Perch' 'Perch' 'Perch']
[[0.   0.05 0.65 0.   0.3  0.   0.  ]
 [0.   0.1  0.3  0.   0.15 0.45 0.  ]
 [0.   0.   0.45 0.25 0.25 0.   0.05]
 [0.   0.15 0.5  0.   0.3  0.   0.05]
 [0.   0.   0.65 0.   0.35 0.   0.  ]]

-> k값을 올려봤자 모델의 정확도만 떨어지고 확률의 다양성도 이전과 큰 차이는 없어보인다.

 

로지스틱 회귀를 이용한 확률 예측

import numpy as np

import matplotlib.pyplot as plt

z = np.arange(-5, 5, 0.1)

phi = 1 / (1 + np.exp(-z))

plt.plot(z, phi)

plt.xlabel('z')

plt.ylabel('phi')

plt.show()

로지스틱 함수의 그래프

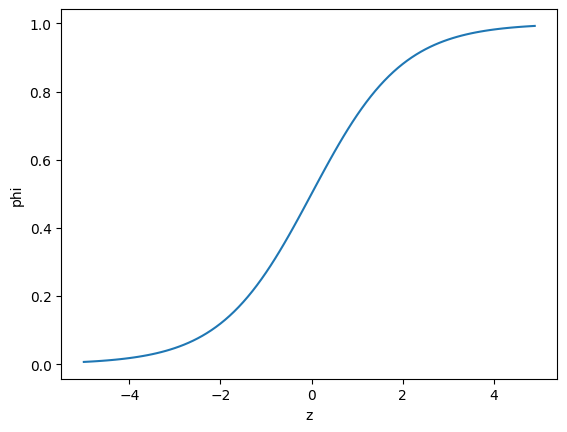
-> 로지스틱 함수를 이용한 값은 연속적이며, 0~1의 범위를 가지기 때문에 확률로 사용하기에 적합해보인다!

 

 

로지스틱 회귀로 이진 분류 수행

char_arr = np.array(['A', 'B', 'C', 'D', 'E'])

print(char_arr[[True, False, True, False, False]])  #True, False 값을 전달하여 넘파이 배열의 행을 선택(boolean indexing)

['A' 'C']

 

bream_smelt_indexes = (train_target  == 'Bream') | (train_target == 'Smelt')  #boolean indexing

train_bream_smelt = train_scaled[bream_smelt_indexes]

target_bream_smelt = train_target[bream_smelt_indexes]

 

from sklearn.linear_model import LogisticRegression #로지스틱 회귀 모델

lr = LogisticRegression()

lr.fit(train_bream_smelt, target_bream_smelt)

 

print(lr.predict(train_bream_smelt[:5]))

print(lr.predict_proba(train_bream_smelt[:5]))

['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
[[0.99759855 0.00240145]
 [0.02735183 0.97264817]
 [0.99486072 0.00513928]
 [0.98584202 0.01415798]
 [0.99767269 0.00232731]]

-> 첫 번째 열이 음성 클래스에 대한 확률, 두 번째 열이 양성 클래스에 대한 확률

 

print(lr.classes_)

['Bream' 'Smelt']

-> 양성 클래스는 도미(smelt)

 

print(lr.coef_, lr.intercept_)

[[-0.4037798  -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]

-> 로지스틱 회귀 모델이 학습한 방정식:

$z = -0.404*(Weight) - 0.576*(Length) - 0.663*(Diagonal)$

                                     $ - 1.013*(Height) - 0.732*(Width) - 2.161  $

 

 여기서 나온 z값을 시그모이드 함수에 넣어주면 확률을 얻을 수 있다.

decisions = lr.decision_function(train_bream_smelt[:5]) #decision_function(): 양성 클래스의 z값 계산

print(decisions)

 

from scipy.special import expit #expit(): 시그모이드 함수

print(expit(decisions)) 

[-6.02927744  3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]

 

로지스틱 회귀로 다중 분류 수행

lr = LogisticRegression(C=20, max_iter=1000)  #logisticRegression의 매개변수 C는 클수록 규제가 완화됨, max_iter는 최대 반복 횟

lr.fit(train_scaled, train_target)

print(lr.score(train_scaled, train_target))

print(lr.score(test_scaled, test_target))

0.9327731092436975
0.925

 

print(lr.predict(test_scaled[:5]))

 

proba = lr.predict_proba(test_scaled[:5])

print(np.round(proba, decimals=3))

['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
[[0.    0.014 0.841 0.    0.136 0.007 0.003]
 [0.    0.003 0.044 0.    0.007 0.946 0.   ]
 [0.    0.    0.034 0.935 0.015 0.016 0.   ]
 [0.011 0.034 0.306 0.007 0.567 0.    0.076]
 [0.    0.    0.904 0.002 0.089 0.002 0.001]]

 

print(lr.classes_)

['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']

 

print(lr.coef_.shape, lr.intercept_.shape)  

(7, 5) (7,)

-> 클래스마다 z값을 각각 계산

 

decision = lr.decision_function(test_scaled[:5])

print(np.round(decision, decimals=2))

 

from scipy.special import softmax

proba = softmax(decision, axis=1) #모든 z값을 softmax함수 처리, axis 지정하지 않으면 모든 배열에 대해 계산

print(np.around(proba, decimals=3))

[[ -6.5    1.03   5.16  -2.73   3.34   0.33  -0.63]
 [-10.86   1.93   4.77  -2.4    2.98   7.84  -4.26]
 [ -4.34  -6.23   3.17   6.49   2.36   2.42  -3.87]
 [ -0.68   0.45   2.65  -1.19   3.26  -5.75   1.26]
 [ -6.4   -1.99   5.82  -0.11   3.5   -0.11  -0.71]]
[[0.    0.014 0.841 0.    0.136 0.007 0.003]
 [0.    0.003 0.044 0.    0.007 0.946 0.   ]
 [0.    0.    0.034 0.935 0.015 0.016 0.   ]
 [0.011 0.034 0.306 0.007 0.567 0.    0.076]
 [0.    0.    0.904 0.002 0.089 0.002 0.001]]

 

---

참고자료

• 박해선, <혼자 공부하는 머신러닝+딥러닝>, 한빛미디어(주), 2022.2.4
• https://hleecaster.com/ml-logistic-regression-concept/

로지스틱회귀(Logistic Regression) 쉽게 이해하기 - 아무튼 워라밸

• https://nittaku.tistory.com/478

5-6. 로지스틱 회귀분석(Logistic Regression)

• https://dnai-deny.tistory.com/9

[라이트 머신러닝]Session 7. 로지스틱 회귀(logistic regression)

• https://m.blog.naver.com/gdpresent/221703566189

Logistic Regression(1) [내가 공부한 머신러닝 #11.]

• https://brunch.co.kr/@linecard/476

앤드류 응의 머신러닝(6-4):로지스틱 회귀 비용함수

• https://lovit.github.io/nlp/machine%20learning/2018/03/24/lasso_keyword/

Logistic regression with L1, L2 regularization and keyword extraction