정규화 모델(릿지,라쏘 모델)

개인적으로 공부하면서 작성한 글이기 때문에, 틀린 내용이 있을 수도 있다는 점 유의하기 바란다. 

 

MSE

 훈련 데이터의 total loss를 의미하는 MSE(training)은 다음과 같이 훈련데이터셋에 대한 모델의 추정값과 참 값의 차이의 제곱으로 나타난다.

 이를 기반으로 테스트 데이터셋의 total loss를 다음과 같이 구할 수 있다. (Irreducible Error는 모델에서 조정하지 못하는 값이다.)

 

 

 

 결론만 말하자면, 테스트 데이터셋의 total loss는 bias와 variance를 조정해 줄일 수 있다. 또한, 이런 테스트 데이터셋의 total loss가 작을수록 좋은 예측 모델이라고 할 수 있다.

 

Bias, Variance

• Bias와 Variance 둘 다, 모델의 loss 또는 error를 의미한다.
• Bias: 타겟 값과 예측 값들의 차이를 의미(추정값의 평균과 참 값들간의 차이)한다. test data를 위한 학습이 덜 된 과소적합의 경우 Bias가 큰 값을 보인다.
• Variance: 예측 값들의 흩어진 정도를 의미(추정값의 평균과 추정값들간의 차)한다. train data에 과하게 fitting된 과대적합의 경우 Variance의 값이 커진다. 

+ Variance는 작은데 Bias가 큰 경우, 영점은 맞춰지지 않았으나 집탄은 잘 됐다고 보면 된다.

 

-> 모델의 복잡도를 높일 경우, Bias 형태의 loss는 0이 되지만 Variance는 그만큼 증가하여 결국 total loss는 증가할 수 있다.

-> 모델의 복잡도를 낮출 경우, Variance 형태의 loss는 0이 되지만 Bias는 그만큼 증가하여 결국 total loss는 증가할 수 있다.

>> 이렇듯 bias와 variance는 서로 상반되어있어 이런 관계 bias-variance trade off(b-v trade off)라 부른다.

 

출처: https://ko.wikipedia.org/wiki/%ED%8E%B8%ED%96%A5-%EB%B6%84%EC%82%B0_%ED%8A%B8%EB%A0%88%EC%9D%B4%EB%93%9C%EC%98%A4%ED%94%84

 

Regularization Method

• error를 줄이는 방법에 Least Squares Method와 Regularization Method가 있는데, 전자는 bias의 값을 줄이는 것만 신경쓰는 방식이고, 후자는 beta 값에 제약을 주어 bias가 조금 증가할 수 는 있어도 variance까지 신경써서 total loss를 줄이는 방식이다.

출처: https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s

• 일반적인 예측 모델에서 테스트 데이터셋의 total loss 최소값을 나타낸 식이다.
• 첫 번째 항은 훈련 데이터셋에서의 MSE(최소제곱법)를 나타내고, 두 번째항은 bias와 관련된 항이라고 이해하면 된다.
• 우리가 모델에서 조절할 수 있는 요소는 두 번째 항의 계수인 λ(람다)인데, 두 항은 서로 상충하기 때문에 람다를 적절히 조절해 total loss의 최소값을 찾아야 한다.  

출처: https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s

 

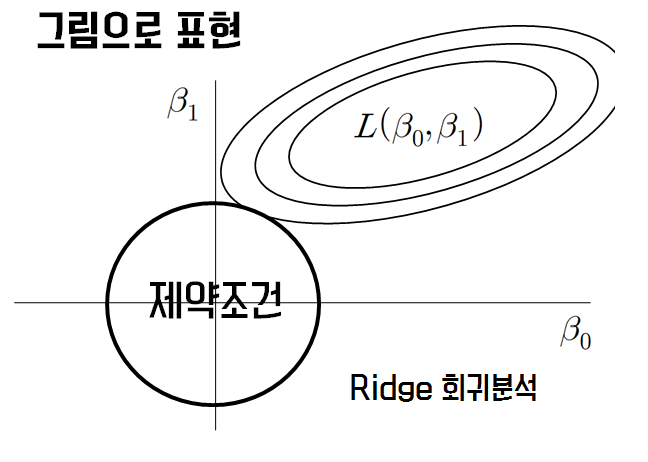
Ridge Regression (릿지 회귀)

• Regularization Method 방법 중 하나로, 회귀 계수의 제곱을 기준으로 규제를 적용한다.

출처: https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s

• MSE의 판별식에 따르면 MSE의 자취는 타원의 형태를 띄며, 회귀 계수의 제약 조건은 원으로 표현되어 그림으로 나타내면 다음과 같다. 따라서, MSE의 최소값은 MSE의 자취가 제약 조건의 원과 만나는 점(제약조건을 만족하는 동시에 에러가 최소)에서의 값과 같다.

출처: http://www.datamarket.kr/xe/index.php?mid=board_BoGi29&document_srl=7176&listStyle=viewer&page=9

 

Lasso Regression (라쏘 회귀)

• Regularization Method 방법 중 하나로, 회귀 계수의 절댓을 기준으로 규제를 적용한다.

• MSE의 판별식에 따르면 MSE의 자취는 타원의 형태를 띄며, 회귀 계수의 제약 조건은 마름모로 표현되어 그림으로 나타내면 다음과 같다. 따라서, MSE의 최소값은 MSE의 자취가 제약 조건의 마름모와 만나는 점(제약조건을 만족하는 동시에 에러가 최소)에서의 값과 같다.

출처: http://www.datamarket.kr/xe/index.php?mid=board_BoGi29&document_srl=7176&listStyle=viewer&page=9

 

 

 

-> 개인적으로 여기에서의 설명보다 벡터 수식으로 직관적으로 보는 것이 더 이해가 잘 됐다. 그 방법은 

https://sypdevlog.tistory.com/111 이 게시물 마지막 부분을 확인하자.

---

참고자료

• https://modulabs-biomedical.github.io/Bias_vs_Variance

Bias vs. Variance 개념 정리

• https://ko.wikipedia.org/wiki/%ED%8E%B8%ED%96%A5-%EB%B6%84%EC%82%B0_%ED%8A%B8%EB%A0%88%EC%9D%B4%EB%93%9C%EC%98%A4%ED%94%84

편향-분산 트레이드오프 - 위키백과, 우리 모두의 백과사전

• https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s
• https://rk1993.tistory.com/entry/Ridge-regression%EC%99%80-Lasso-regression-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0

Ridge regression(릿지 회귀)와 Lasso regression(라쏘 회귀) 쉽게 이해하기