[KHUDA 4th] 머신러닝 2주차 기초 세션 (08.10)

토의 내용 정리

 

각 조에서 나온 질문들을 조원들과 상의하면서 답변하는 시간을 가졌다. 나는 2조의 질문에 대한 답변을 작성했고, 나머지는 피드백 정도만! 파란색 글자는 내가 작성한 의견이다.

 

1조: 특성의 갯수를 계속 늘리고 규제를 적용한다면 모델의 성능은 계속 좋아지는 것인가? 아니면 특성의 갯수에도 적절한 값이 존재할까?

 불필요한 특성이 많아질 수록 그것을 처리하기 위해 규제가 세진다면, 필요한 특성들에 대해서도 규제가 과하게 적용되어 악영향을 줄 수 있을 것 같다. (+ 처리할 연산이 많아짐.)

-> 라고 생각을 했었지만, 요즘 트렌드는 되는대로 특성을 늘려서 때려박고, 규제를 적용시키는 것이라고 한다! 따라서, 현재까지는 특성의 양이 많아지면서 생기는 문제보다는 성능이 향상되는 이점이 더 많은 것으로 추정된다.

 

 

 

 

2조: 특성을 생성할때 설명력이 있는 특성(키와 몸무게 특성이 존재할때 bmi특성을 만드는 행위)을 만드는게 좋은가? 혹은 모델의 성능이 높은 특성을 선택하는게 좋은가? (모델의 설명력과 성능이 상반된다고 가정할때)

 설명력이 부족한 특성을 사용하여 모델을 학습했을 때, 나온 결과의 처리과정을 설명하기 어렵다. 이렇듯 결과만 보고 알고리즘을 이해하기가 힘들다는 단점이 있긴 하지만, 많은 양의 데이터를 넣었을 때, 개발자가 굳이 규칙을 파악하지 않아도 데이터만으로 높은 정확도를 가지는 예측 결과를 이끌어내는 딥러닝의 장점을 생각했을 때, 성능이 높은 특성을 선택하는 것이 좋다고 생각한다. 또한, 설명력이 없는 데이터셋은 기존의 특성을 조합하는 방식과 같이 데이터의 규모를 키우기가 좋다는 장점도 가지고 있다.

대신 설명력이 부족한 특성을 사용할 경우 데이터의 양이 충분히 많아야 한다고 생각한다. >>결국에 성능이 나오지 않으면 머신러닝의 의미가 사라진다.

-> 내가 작성한 답변!!

 

3조: 원핫 인코딩을 진행할 때 클래스의 값이 너무 많으면 어떡하나 그러면 벡터의 크기가 너무 커지지 않나요?

→ 차원축소 과정을 거쳐 그 단점을 개선할 수 있다. (PCA, skip-gram, GloVe 등등…)

→ 클래스의 값이 너무 커지면 원핫 인코딩 방식은 공간적 낭비가 일어난다. 단어를 다루고 있다면 단어를 밀집 벡터의 형태로 표현하는 방법인 워드 임베딩 과정을 진행하면 된다. 임베딩 벡터를 사용하면 원핫벡터와 다르게 저차원이고, 0과 1이 아닌 실수로 나타난다.

 

4조: 테스트 세트에 사이킷런 변환기를 사용할 때, 왜 훈련 세트에서 학습한 변환기를 사용해야 하는가?

모델은 변환된 데이터를 가지고 학습했기 때문에 정답을 찾아가는 과정이 그 변환된 데이터에 맞춰져 있을 것이다. 그렇기 때문에 테스트 세트에도 훈련 세트에 적용한 변환 방식을 그대로 적용해서 성능 평가를 진행해야 한다. 만일 변환되지 않은 테스트 세트로 성능을 측정하면 낮은 성능을 보이게 될 것이다.

테스트 세트에 사이킷런 변환기를 사용할 때 무조건 훈련 세트에서 학습한 변환기를 사용해야 하는 것은 아니다. 예를 들면 polynomialfeatures 클래스는 fit 매서드에서 만들 특성의 조합을 준비하기만 하고 별도의 통계 값을 구하지 않기 때문에 테스트 세트를 변환 해도 상관 없다. 하지만 훈련 세트를 기준으로 테스르세트를 변환 하는 사용하는 것이 익숙해야 한다는 것이다.

 

5조: 선형 모델에서 모델의 복잡도를 줄이는 것보다 규제를 적용하는 것이 더 효과적인 이유가 따로 있을지, 경우에 따라 규제를 적용하는 것보다 모델의 복잡도를 수정하는 것이 더 효과적인 경우가 따로 있는지?

→ 선형모델의 복잡도를 줄이는 방법 중 하나가 규제입니다. 규제는 복잡도를 줄여 일반화하는 성능을 향상시키는 것입니다. 규제의 장점으로는 모델을 일반화한 예측을 만들어 편향을 줄일 수 있습니다.

 

 

2주차 과제 공통 질문

 

2주차 비대면 과제로 나왔던 공통 질문에 대한 답변을 세션 들어가기 전에 혼자 정리해본 글이다. 

 

과대적합과 과소적합의 기준은 무엇인가?

• 과소적합: 훈련 세트보다 테스트 세트의 점수가 높거나 / 두 점수 모두 너무 낮은 경우

과소적합의 문제는 모델의 복잡도가 낮을 때 발생하므로, 모델이 테스트 세트의 디테일한 구조를 제대로 잡아내지 못했는지 확인해야 한다.

• 과대적합: 높은 훈련 세트의 점수에 비해 테스트 세트에서 점수가 굉장히 낮은 경우

과대적합의 경우 모델이 훈련 세트에 대해서 과도하게 학습되어 발생하므로, 과소적합의 경우와 반대로 훈련 세트의 학습 과정에서 데이터의 노이즈까지 학습되는 문제가 발생하지는 않았는지 확인해야 한다.

 

릿지와 라쏘 회귀는 각각 어느 상황에서 사용하는 것이 적합한지, 책에서 릿지 회귀를 더 선호한다고 말한 이유는 무엇인지?

(다중공선성(multicollinearity)이란 독립 변수의 일부가 다른 독립 변수의 조합으로 표현될 수 있는 경우)

 

• 릿지는 변수 간 상관관계가 높은 상황(collinearity)에서 좋은 예측 성능을 보이며, 라쏘는 같은 상황에서 성능이 떨어진다.
• 라쏘는 불필요한 특성들의 가중치를 0으로 만들어 해당 특성을 제외하는 특징을 가지고 있어, 특성 선택이 중요한 경우에 유용하다.
• 릿지는 라쏘와 다르게 가중치를 0에 가깝게 제한하지만 0으로 만들지는 않는다. 따라서 모든 특성이 적절히 고려되면서 모델의 안정성을 유지하기에 용이하다.

 

릿지와 라쏘 이외의 다른 규제 모델은 무엇이 있는가?

• Elastic Net = Ridge + Lasso (L1과 L2), 상관관계 높은 변수들 동시에 선택
• Fused Lasso, 인접한 변수들 동시에 선택 → signal/profile/spectra

출처:  https://www.youtube.com/watch?v=sGTWFCq5OKM

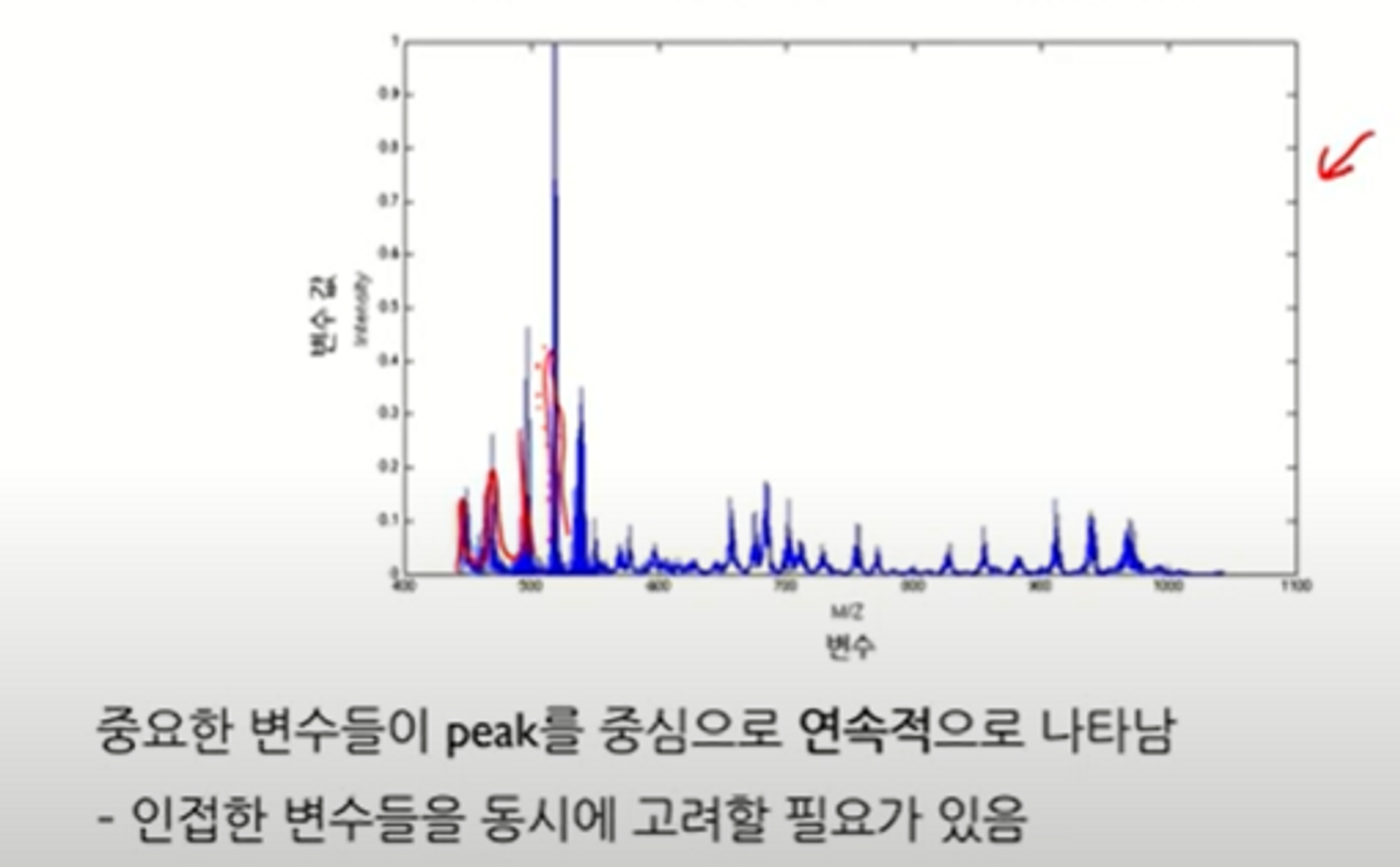
• Group Lasso, 사용자가 정의한 그룹 단위로 변수 선택
• Grace, 사용자가 정의한 그래프의 연결 관계에 따라 변수 선택

 

K 값을 조정하는 것 외에, 과대적합/과소적합을 해결하는 방법은 무엇이 있는가?

• 데이터의 양을 조정해서, 모델의 복잡도를 조절하는 방법이 있다.
• 데이터의 정규화(릿지, 라쏘)를 통해서 과대적합/과소적합을 해결

 

특성끼리 곱해 새로운 특성을 만든다는 것에 대한 의미는 무엇인가?

• 기존에 있던 특성끼리의 곱을 통해 새로운 특성을 추가함으로써, 기존의 특성과 관계 없는 특성의 샘플을 새로 구할 필요성이 사라진다.
• 서로 다른 특성들 간의 상호작용을 고려할 수 있다. ex) 길이와 무게라는 특성이 있을 때, 길이와 무게가 동시에 영향을 미치는 상황을 모델이 학습할 수 있다.

 

 

2주차 세션 발표 내용 정리

 

2주차 세션에서 4조가 발표했던 내용중에 이해가 안 됐거나, 따로 정리하고 싶었던 내용들을 정리해봤다. 

 

놈(Norm)

• 놈: 벡터의 크기(magnitude) 혹은 길이(length)를 측정하는 방법
• L1 norm: 맨해튼 놈(Manhattan norm) 혹은 택시 놈(Taxicab norm) -> 맨해튼  거리로 계산
• L2 norm: 유클리드 놈(Euclidean norm) -> 유클리드 거리(직선 거리)로 계산

 

그래디언트

• f는 스칼라 함수

출처: https://ko.wikipedia.org/wiki/%EB%8D%B8_(%EC%97%B0%EC%82%B0%EC%9E%90)

 

+ 사실 놈이나 그래디언트도 배운 개념들인데, 군복무하면서 다 까먹은 거 같아서 다시 정리해봤다..ㅠ

 

목적 함수

• 목적 함수(Object Function): 모델을 학습해 최적하하고자 하는 함수이다. 확률 관점에서는 목적 함수를 최대화, error 관점에서는 목적 함수를 최소화해야 한다.

 

경사하강법

• 경사 하강법(Gradient descent)은1차 근삿값  발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다.

이미지 출처 :  medium.com

• 목적 함수 그래프가 위와 같을 때, 목적 함수를 미분시켜서 loss가 최소화되는 지점까지 계속해서 이동하는 것이 경사하강법이다.

 

L2 규제보다 L1규제를 사용할 때 가중치가 0이 될 확률이 높은 이유?

https://sypdevlog.tistory.com/110 -> 해당 게시물에서 L1 규제의 규제 범위는 마름모 형태, L2 규제의 규제 범위는 원의 형태라고 언급했었다, L1 규제는 규제 범위와 만나는 점이 마름모의 꼭짓점이 될 확률이 높기 때문에 가중치가 0이 될 확률이 L2 규제보다 높아진다.

-> 수식으로 직관적으로 이해해보자.

L2 규제와 L1규제

-> L2에서 가중치는 규제 적용 이전 가중치의 계수인 1-2ρλ만 0이 되지 않으면 0.98세타, 0.99세타와 같이 비율을 줄인 자신을 빼는 연산이 계속되기 때문에 0에는 수렴하지만 0이 되기는 힘들다.

-> L1에서는 sign함수에 의해서 직관적으로 0에 계속 가까워지는 형태이기 때문에, 가중치가 0이 되는 경우가 많다.

 

---

참고자료

• https://datascienceschool.net/03%20machine%20learning/06.04%20%EB%8B%A4%EC%A4%91%EA%B3%B5%EC%84%A0%EC%84%B1%EA%B3%BC%20%EB%B3%80%EC%88%98%20%EC%84%A0%ED%83%9D.html

6.4 다중공선성과 변수 선택 — 데이터 사이언스 스쿨

• https://www.youtube.com/watch?v=sGTWFCq5OKM

• https://bskyvision.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%99-%EB%86%88norm%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80

[선형대수학] 놈(norm)이란 무엇인가?

• https://ok-lab.tistory.com/171

Object Function, Cost Function, Loss Fuction

• https://only-wanna.tistory.com/entry/%EB%AA%A9%EC%A0%81-%ED%95%A8%EC%88%98%EC%99%80-%EC%B5%9C%EC%A0%81%ED%99%94

목적 함수(Objective function)와 최적화(Optimization)

• https://dotiromoook.tistory.com/25

[Deep Learning] 경사하강법 (Gradient Descent) 이란