Chapter 03-3: 특성 공학과 규제

여러 특성을 사용한 다중 회귀에 대해 학습하고,
복잡한 모델의 과대적합을 막기 위해 릿지와 라쏘 회귀를 이용해보자.

 

 

다중 회귀

• 다중 회귀(multiple regression): 여러 개의 특성을 사용하는 선형 회귀 모델. 특성이 많으면 선형 모델은 강력한 성능을 발휘한다.
• 특성 공학(feature engineering): 기존의 특성을 사용해 새로운 특성을 만드는 일련의 작업 과정이다.

데이터 준비

import pandas as pd

df = pd.read_csv('https://bit.ly/perch_csv_data') #pandas를 사용해 농어 데이터를 데이터프레임에 저장

perch_full = df.to_numpy()  #데이터프레임에 저장된 csv 파일을 numpy 배열로 바꾸는 method

print(perch_full)  #length, height, width 데이터 출력

 

[[ 8.4   2.11  1.41]
 [13.7   3.53  2.  ]
 [15.    3.82  2.43]
 [16.2   4.59  2.63]
 [17.4   4.59  2.94]
 [18.    5.22  3.32]
 [18.7   5.2   3.12]
 [19.    5.64  3.05]
 [19.6   5.14  3.04]
 [20.    5.08  2.77]
 [21.    5.69  3.56]
 [21.    5.92  3.31]
 [21.    5.69  3.67]
 [21.3   6.38  3.53]
 [22.    6.11  3.41]
 [22.    5.64  3.52]
 [22.    6.11  3.52]
 [22.    5.88  3.52]
 [22.    5.52  4.  ]
 [22.5   5.86  3.62]
 [22.5   6.79  3.62]
 [22.7   5.95  3.63]
 [23.    5.22  3.63]
 [23.5   6.28  3.72]
 [24.    7.29  3.72]
 [24.    6.38  3.82]
 [24.6   6.73  4.17]
 [25.    6.44  3.68]
 [25.6   6.56  4.24]
 [26.5   7.17  4.14]
 [27.3   8.32  5.14]
 [27.5   7.17  4.34]
 [27.5   7.05  4.34]
 [27.5   7.28  4.57]
 [28.    7.82  4.2 ]
 [28.7   7.59  4.64]
 [30.    7.62  4.77]
 [32.8  10.03  6.02]
 [34.5  10.26  6.39]
 [35.   11.49  7.8 ]
 [36.5  10.88  6.86]
 [36.   10.61  6.74]
 [37.   10.84  6.26]
 [37.   10.57  6.37]
 [39.   11.14  7.49]
 [39.   11.14  6.  ]
 [39.   12.43  7.35]
 [40.   11.93  7.11]
 [40.   11.73  7.22]
 [40.   12.38  7.46]
 [40.   11.14  6.63]
 [42.   12.8   6.87]
 [43.   11.93  7.28]
 [43.   12.51  7.42]
 [43.5  12.6   8.14]
 [44.   12.49  7.6 ]]

import numpy as np

perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,

       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,

       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,

       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,

       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,

       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,

       1000.0])

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)

 

사이킷런의 변환기

• 변환기(transformer): 특성을 만들거나 전처리하기 위해 사이킷런에서 제공하는 클래스를 의미한다.

from sklearn.preprocessing import PolynomialFeatures  #변환기 PolynomialFeatures

poly = PolynomialFeatures(include_bias=False) #include_bias=False로 설정하면 절편 항 제거, 사이킷런의 선형 모델은 자동으로 절편을 추가하므로 이와 같이 설정

poly.fit(train_input) #새롭게 만들 특성 조합을 찾는다.

train_poly = poly.transform(train_input)  #실제로 데이터를 변환

test_poly = poly.transform(test_input)

print(train_poly.shape)

poly.get_feature_names_out()  #9개의 특성이 각각 어떤 입력의 조합으로 만들어졌는지 확인

(42, 9)
array(['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2',
       'x2^2'], dtype=object)

 

다중 회귀 모델 훈련

from sklearn.linear_model import LinearRegression

lr = LinearRegression()

lr.fit(train_poly, train_target)

print(lr.score(train_poly, train_target))

print(lr.score(test_poly, test_target))

0.9903183436982125
0.9714559911594111

-> 테스트 세트에 대한 점수는 높아지지 않았지만, 과소적합 문제는 해결

 

+ 별도로 정규화의 중요성에 대해 정리해봄. ridge 모델 학습 과정까지 보고 읽어보는 것을 추천한다.

 아래 규제의 과정에서 알 수 있듯이, 특성마다 스케일의 차이가 있기 때문에 정규화를 진행시켜야 한다. 따라서, 필자는 변환기에 의해 특성이 늘어난 train_poly 데이터셋을 정규화시켜 모델을 학습해봤다.

from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)  
train_scaled = ss.transform(train_poly) #표준점수로 변환
test_scaled = ss.transform(test_poly) #표준점수로 변환
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))

0.9903183436982124
0.9714559911594131

  정규화 전과 차이가 없어보이지만, 아주 미묘하게 정규화를 진행한 후의 모델이 테스트세트에서 높은 점수를 보인다. 하지만, 이는 모델의 성능에 큰 영향을 끼치지 못하는 아주 미미한 차이이다.

 

  그렇다면 차수가 높아진 다중 회귀 모델에서 정규화를 진행하지 않으면 어떤 차이가 발생할까?

from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_poly, train_target)
print(ridge.score(train_poly, train_target))
print(ridge.score(test_poly, test_target))

0.9970688863268867
0.9149349567850471

  정규화를 진행한 모델과 테스트 세트에서의 점수가 약 6% 정도 차이가 난다. 

 

-> 결론적으로, 변환기를 이용해 특성을 늘리는 상황에서, 차수가 낮은 상황에 비해서 차수가 높은 상황이 될수록 정규화의 중요성은 커진다는 것을 알 수 있다.

 

고차항 다중 회귀 모델

poly = PolynomialFeatures(degree=5, include_bias=False) #매개변수 degree로 고차항의 최대 차수 지정 가능

poly.fit(train_input)

train_poly = poly.transform(train_input)

test_poly = poly.transform(test_input)

print(train_poly.shape)

(42, 55)

-> train_poly 배열의 열의 개수가 특성의 개수, 특성의 개수가 55개

 

lr.fit(train_poly, train_target)

print(lr.score(train_poly, train_target))

print(lr.score(test_poly, test_target))

0.9999999999996433
-144.40579436844948

-> 특성의 개수를 늘려 훈련 세트에 대해 거의 완벽하게 학습할 수 있게 되었지만, 이로 인해서 훈련 세트에 너무 과대적합되는 문제가 발생

 

규제

• 규제(regularization): 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 방해하는 것
• 선형 회귀 모델에 규제를 추가한 모델에는 릿지(ridge)와 라쏘(lasso)가 있다. 두 모델 모두 계수의 크기를 줄인다.

릿지, 라쏘 회귀에 관한 자세한 설명은 여기서 -> https://sypdevlog.tistory.com/110

from sklearn.preprocessing import StandardScaler

ss = StandardScaler()

ss.fit(train_poly)  #해당 과정을 꼭 거쳐야 함

train_scaled = ss.transform(train_poly) #표준점수로 변환  

test_scaled = ss.transform(test_poly) #표준점수로 변환

 

 

릿지 회귀

• 릿지(ridge): 선형 모델의 계수를 작게 만들어 과대적합을 완화시킨다. 릿지는 비교적 효과가 좋아 널리 사용
• 계수를 제곱한 값을 기준으로 규제 적용

from sklearn.linear_model import Ridge

ridge = Ridge()

ridge.fit(train_scaled, train_target)

print(ridge.score(train_scaled, train_target))

print(ridge.score(test_scaled, test_target))

0.9896101671037343
0.9790693977615387

-> 정규화를 진행하지 않았을 때 어떤 점수가 나왔을지 궁금하다면, 위 다중회귀모델 훈련 파트의 접은 글을 확인해보자!

 

alpha 매개변수

• 릿지와 라쏘 모델을 사용할 때 alpha 매개변수로 규제의 강도를 임의로 조절할 수 있다.
• alpha 값이 크면 규제 강도가 세지므로, 계수 값을 더 줄이고 조금 더 과소적합되도록 유도
• alpha 값이 작으면 계수를 줄이는 역할이 줄어들고 선형 회귀 모델과 유사해지므로 과대적합될 가능성이 큼

import matplotlib.pyplot as plt

train_score = []  #alpha 값을 바꿀 때마다 score() 결과를 저장할 리스트

test_score = [] #alpha 값을 바꿀 때마다 score() 결과를 저장할 리스트

 

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100] #alpha 값마다 R^2 그래프를 그려 최적(훈련 세트와 테스트 세트의 점수가 가장 가까운 지점)의 alpha 값 탐색

for alpha in alpha_list:

  ridge = Ridge(alpha=alpha)

  ridge.fit(train_scaled, train_target)

  train_score.append(ridge.score(train_scaled, train_target))

  test_score.append(ridge.score(test_scaled, test_target))

 

plt.plot(np.log10(alpha_list), train_score) #0.001부터 100까지의 x축이 동일한 간격을 가지도록 log 함수로 변형

plt.plot(np.log10(alpha_list), test_score)  #0.001부터 100까지의 x축이 동일한 간격을 가지도록 log 함수로 변형

plt.xlabel('alpha')

plt.ylabel('R^2')

plt.show()

-> alpha 값이 작을 때는 과대적합, 클 때는 과소적합의 경향을 보인다. 최적의 alpha 값은 0.1

ridge = Ridge(alpha=0.1)  #최적의 alpha 값으로 모델을 훈련

ridge.fit(train_scaled, train_target)

print(ridge.score(train_scaled, train_target))

print(ridge.score(test_scaled, test_target))

0.9903815817570367
0.9827976465386928

 

라쏘 회귀

• 라쏘(lasso): 릿지 모델과 유사하게 계수의 크기를 줄이지만, 라쏘는 아예 0으로 만들 수도 있다.
• 계수의 절댓값을 기준으로 규제 적용

from sklearn.linear_model import Lasso

lasso = Lasso()

lasso.fit(train_scaled, train_target)

print(ridge.score(train_scaled, train_target))

print(lasso.score(test_scaled, test_target))

0.9903815817570367
0.9800593698421883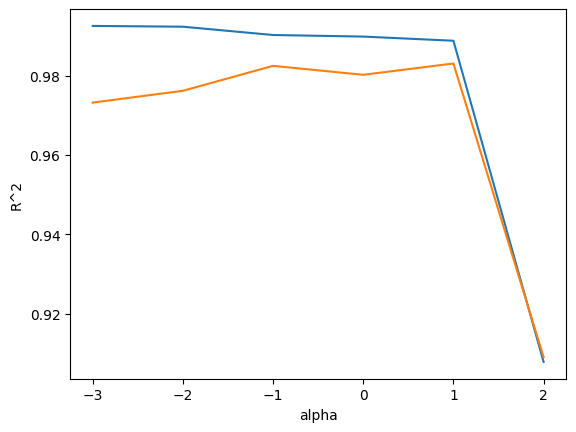

train_score = []

test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:

  lasso = Lasso(alpha=alpha, max_iter=10000)  #ConvergenceWarning: 최적의 계수를 찾기 위한 반복적 계산의 반복 횟수가 부족할 때 발생하는 경고, max_iter: 반복 횟수를 충분히 늘리기 사용

  lasso.fit(train_scaled, train_target)

  train_score.append(lasso.score(train_scaled, train_target))

  test_score.append(lasso.score(test_scaled, test_target))

 

plt.plot(np.log10(alpha_list), train_score)

plt.plot(np.log10(alpha_list), test_score)

plt.xlabel('alpha')

plt.ylabel('R^2')

plt.show()

-> alpha 값이 작을 때는 과대적합, 클 때는 과소적합의 경향을 보인다. 최적의 alpha 값은 10

lasso = Lasso(alpha=10)

lasso.fit(train_scaled, train_target)

print(lasso.score(train_scaled,train_target))

print(lasso.score(test_scaled, test_target))

0.9888067471131867
0.9824470598706695

print(np.sum(lasso.coef_ ==0))  #라쏘 모델이 0으로 만든 계수의 개수

-> np.sum() 함수는 True를 1로, False를 0으로 인식

40

 

---

참고자료

• 박해선, <혼자 공부하는 머신러닝+딥러닝>, 한빛미디어(주), 2022.2.4
• https://shacoding.com/2022/03/19/%ED%86%B5%EA%B3%84%ED%95%99-%EC%A0%95%EA%B7%9C%ED%99%94%EC%99%80-%ED%91%9C%EC%A4%80%ED%99%94%EC%9D%98-%ED%95%84%EC%9A%94%EC%84%B1-with-machine-learning/