| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 오블완
- 티스토리챌린지
- LLM
- ChatGPT
- 딥러닝
- 지도학습
- LG Aimers 4th
- deep learning
- PCA
- regression
- 분류
- 회귀
- AI
- gpt
- 머신러닝
- 해커톤
- Classification
- Machine Learning
- LG Aimers
- supervised learning
- LG
- GPT-4
- OpenAI
Archives
- Today
- Total
SYDev
[Data Structure] Chapter 11-2: 이진 탐색 트리 본문
Data Structure & Algorithm/Data Structure
[Data Structure] Chapter 11-2: 이진 탐색 트리
시데브 2023. 9. 12. 18:54이진 탐색 트리에 대해 이해하고, 이를 구현해보자.
이진 탐색 트리
- 이진 탐색 트리(Binary Search Tree): '이진 트리'에 '데이터의 저장 규칙'을 더해놓은 탐색 알고리즘이다.
- 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.


이진 탐색 트리의 삽입과 탐색 구현
- 이전에 구현한 BinaryTree2.h와 BinaryTree2.c를 이용한다.
파일명: BinarySearchTree.h
#ifndef __BINARY_SEARCH_TREE_H__
#define __BINARY_SEARCH_TREE_H__
#include "BinaryTree2.h"
typedef BTData BSTData;
//BST 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
//노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
//BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
//BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
#endif
파일명: BinarySearchTree.c
#include <stdio.h>
#include "BinaryTree2.h"
#include "BinarySearchTree.h"
//BST 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot)
{
*pRoot = NULL;
}
//노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst)
{
return bst->data;
}
//BST를 대상으로 데이터 저장(노드의 생성과정 포함)
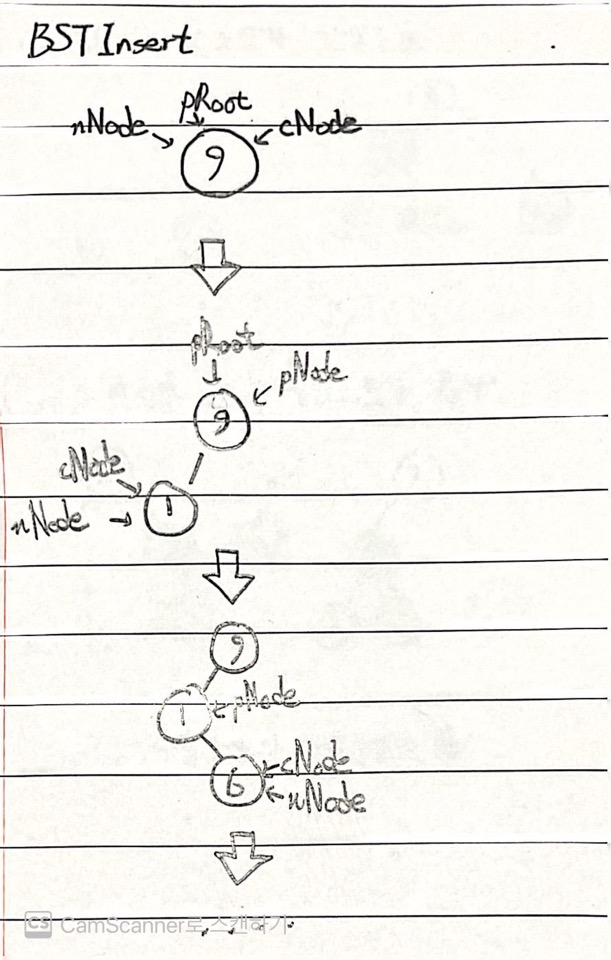
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL;
BTreeNode * cNode = *pRoot;
BTreeNode * nNode = NULL;
//저장 위치를 찾는 while문
while(cNode != NULL)
{
if(data == GetData(cNode))
return;
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
nNode = MakeBTreeNode();
SetData(nNode, data);
//생성된 nNode를 저장 위치에 지정
if(pNode != NULL)
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else
{
*pRoot = nNode;
}
}
//BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst;
BSTData cd;
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL;
}
파일명: BinarySearchTreeMain.c
#include <stdio.h>
#include "BinarySearchTree.h"
int main(void)
{
BTreeNode * bstRoot;
BTreeNode * sNode;
BSTMakeAndInit(&bstRoot);
BSTInsert(&bstRoot, 9);
BSTInsert(&bstRoot, 1);
BSTInsert(&bstRoot, 6);
BSTInsert(&bstRoot, 2);
BSTInsert(&bstRoot, 8);
BSTInsert(&bstRoot, 3);
BSTInsert(&bstRoot, 5);
BSTInsert(&bstRoot, 1);
sNode = BSTSearch(bstRoot, 1);
if(sNode == NULL)
printf("탐색 실패 \n");
else
printf("탐색에 성공한 키의 값: %d \n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 4);
if(sNode == NULL)
printf("탐색 실패 \n");
else
printf("탐색에 성공한 키의 값: %d \n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 6);
if(sNode == NULL)
printf("탐색 실패 \n");
else
printf("탐색에 성공한 키의 값: %d \n", BSTGetNodeData(sNode));
sNode = BSTSearch(bstRoot, 7);
if(sNode == NULL)
printf("탐색 실패 \n");
else
printf("탐색에 성공한 키의 값: %d \n", BSTGetNodeData(sNode));
return 0;
}탐색에 성공한 키의 값: 1
탐색 실패
탐색에 성공한 키의 값: 6
탐색 실패
이진 탐색 트리의 삭제 구현
- 루트 노드가 삭제되는 경우를 고려해야 한다
- 자식 노드의 개수에 따라서 경우가 세 가지로 나뉜다.
- 새로운 함수인 Remove~(노드를 삭제), Change~(Make~와 다르게 메모리 소멸과정 x)를 추가한다.
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
- 왼쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값 반환
BTreeNode * RemoveRightSubTree(BTreeNode * bt);
- 오른쪽 자식 노드를 트리에서 제거, 제거된 노드의 주소 값 반환
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
- 메모리 소멸을 수반하지 않고 main의 왼쪽 자식 노드를 변경
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
- 메모리 소멸을 수반하지 않고 main의 오른쪽 자식 노드를 변경


파일명: BinaryTree3.h
#ifndef __BINARY_TREE3_H__
#define __BINARY_TREE3_H__
typedef int BTData;
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode * bt);
void SetData(BTreeNode * bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
typedef void (*VisitFuncPtr)(BTData data);
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action);
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action);
BTreeNode * RemoveLeftSubTree(BTreeNode * bt);
BTreeNode * RemoveRightSubTree(BTreeNode * bt);
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endif
파일명: BinaryTree3.c
#include "BinaryTree3.h"
#include <stdio.h>
#include <stdlib.h>
BTreeNode * MakeBTreeNode(void)
{
BTreeNode * newNode = (BTreeNode*)malloc(sizeof(BTreeNode));
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}
void PreorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
action(bt->data);
PreorderTraverse(bt->left, action);
PreorderTraverse(bt->right, action);
}
void InorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
InorderTraverse(bt->left, action);
action(bt->data);
InorderTraverse(bt->right, action);
}
void PostorderTraverse(BTreeNode * bt, VisitFuncPtr action)
{
if(bt == NULL)
return;
PostorderTraverse(bt->left, action);
PostorderTraverse(bt->right, action);
action(bt->data);
}
BTreeNode * RemoveLeftSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->left;
bt->left = NULL;
}
return delNode;
}
BTreeNode * RemoveRightSubTree(BTreeNode * bt)
{
BTreeNode * delNode;
if(bt != NULL)
{
delNode = bt->right;
bt->right = NULL;
}
return delNode;
}
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
main->left = sub;
}
void ChangeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
main->right = sub;
}
파일명: BinarySearchTree2.h
#ifndef __BINARY_SEARCH_TREE_H__
#define __BINARY_SEARCH_TREE_H__
#include "BinaryTree3.h"
typedef BTData BSTData;
//BST 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot);
//노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst);
//BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data);
//BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target);
//트리에서 노드를 제거하고 제거된 노드의 주소 값 반환
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target);
//이진 탐색 트리에 저장된 모든 노드의 데이터를 출력
void BSTShowAll(BTreeNode * bst);
#endif
파일명: BinarySearchTree2.c
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree3.h"
#include "BinarySearchTree2.h"
//BST 생성 및 초기화
void BSTMakeAndInit(BTreeNode ** pRoot)
{
*pRoot = NULL;
}
//노드에 저장된 데이터 반환
BSTData BSTGetNodeData(BTreeNode * bst)
{
return bst->data;
}
//BST를 대상으로 데이터 저장(노드의 생성과정 포함)
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL;
BTreeNode * cNode = *pRoot;
BTreeNode * nNode = NULL;
//저장 위치를 찾는 while문
while(cNode != NULL)
{
if(data == GetData(cNode))
return;
pNode = cNode;
if(GetData(cNode) > data)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
nNode = MakeBTreeNode();
SetData(nNode, data);
//생성된 nNode를 저장 위치에 지정
if(pNode != NULL)
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else
{
*pRoot = nNode;
}
}
//BST를 대상으로 데이터 탐색
BTreeNode * BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst;
BSTData cd;
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target < cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL;
}
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target)
{
BTreeNode * pVRoot = MakeBTreeNode();
BTreeNode * pNode = pVRoot;
BTreeNode * cNode = *pRoot;
BTreeNode * dNode;
ChangeRightSubTree(pVRoot, *pRoot); //루트 노드가 삭제될 경우를 대비하여 루트 노드의 pNode를 지정
while(cNode != NULL && GetData(cNode) != target)
{
pNode = cNode;
if(target < GetData(cNode))
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
if(cNode == NULL)
return NULL;
dNode = cNode;
//Case 1.
if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL)
{
if(GetLeftSubTree(pNode) == dNode)
RemoveLeftSubTree(pNode);
else
RemoveRightSubTree(pNode);
}
//Case 2.
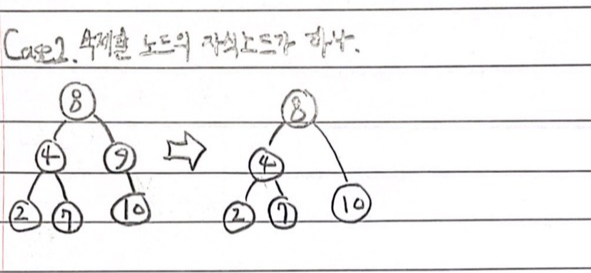
else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL)
{
BTreeNode * dcNode;
if(GetLeftSubTree(dNode) != NULL)
dcNode = GetLeftSubTree(dNode);
else
dcNode = GetRightSubTree(dNode);
if(GetLeftSubTree(pNode) == dNode)
ChangeLeftSubTree(pNode, dcNode);
else
ChangeRightSubTree(pNode, dcNode);
}
//Case 3.
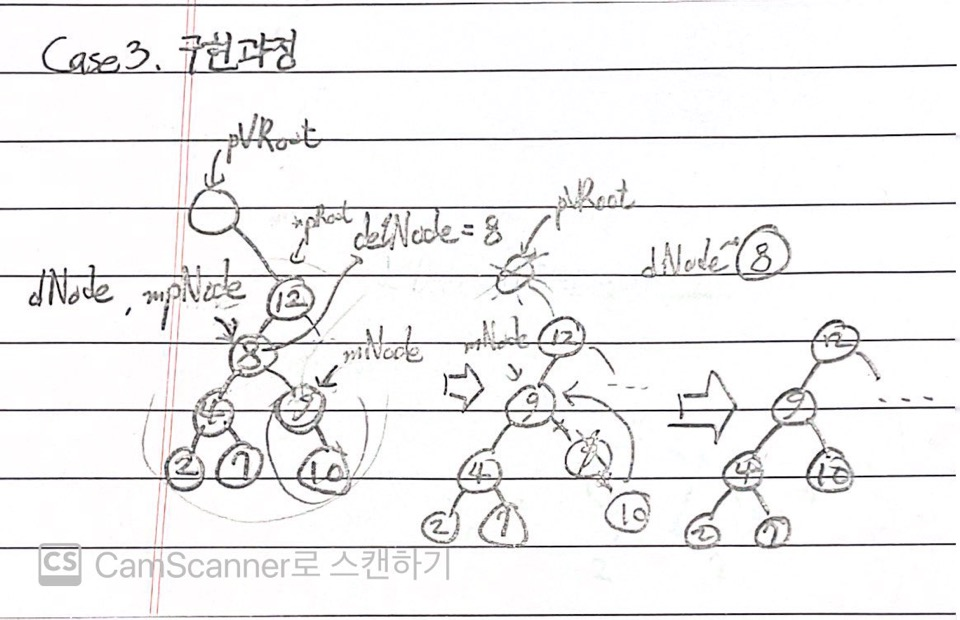
else
{
BTreeNode * mNode = GetRightSubTree(dNode);
BTreeNode * mpNode = dNode;
int delData;
while(GetLeftSubTree(mNode) != NULL)
{
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
delData = GetData(dNode);
SetData(dNode, GetData(mNode)); //루트 노드에 대체 노드 데이터 저장
// 대체 노드의 부모 노드와 자식 노드 연결
if(GetLeftSubTree(mpNode) == mNode) //while을 한 바퀴라도 돈 경우!!
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
else //while을 한 바퀴도 돌지 않은 경우!!
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
dNode = mNode;
SetData(dNode, delData);
}
//삭제된 노드가 루트 노드일 때 추가적인 처리
if(GetRightSubTree(pVRoot) != *pRoot)
*pRoot = GetRightSubTree(pVRoot);
free(pVRoot);
return dNode;
}
void ShowIntData(int data)
{
printf("%d ",data);
}
void BSTShowAll(BTreeNode * bst)
{
InorderTraverse(bst, ShowIntData);
}
파일명: BinarySearchTreeDelMain.c
#include <stdio.h>
#include <stdlib.h>
#include "BinarySearchTree2.h"
int main(void)
{
BTreeNode * bstRoot;
BTreeNode * sNode;
BSTMakeAndInit(&bstRoot);
BSTInsert(&bstRoot, 5);
BSTInsert(&bstRoot, 8);
BSTInsert(&bstRoot, 1);
BSTInsert(&bstRoot, 6);
BSTInsert(&bstRoot, 4);
BSTInsert(&bstRoot, 9);
BSTInsert(&bstRoot, 3);
BSTInsert(&bstRoot, 2);
BSTInsert(&bstRoot, 7);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 3);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 8);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 1);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
sNode = BSTRemove(&bstRoot, 6);
free(sNode);
BSTShowAll(bstRoot); printf("\n");
return 0;
}1 2 3 4 5 6 7 8 9
1 2 4 5 6 7 8 9
1 2 4 5 6 7 9
2 4 5 6 7 9
2 4 5 7 9

- 윤성우, <윤성우의 열혈 자료구조>, 오렌지미디어, 2022.04.11
728x90
반응형
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] Chapter 13-1: 빠른 탐색을 보이는 해쉬 테이블 (1) | 2023.09.17 |
|---|---|
| [Data Structure] Chapter 12: 균형 잡힌 이진 탐색 트리 - AVL 트리 (0) | 2023.09.13 |
| [Data Structure] Chapter 11-1: 탐색의 이해와 보간 탐색 (1) | 2023.09.11 |
| [Data Structure] Chapter 10-2: 복잡하지만 효율적인 정렬 알고리즘 (0) | 2023.09.11 |
| [Data Structure] Chapter 10-1: 단순한 정렬 알고리즘 (0) | 2023.09.08 |




