| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 해커톤
- 오블완
- LLM
- PCA
- LG Aimers
- AI
- LG Aimers 4th
- 딥러닝
- deep learning
- ChatGPT
- 머신러닝
- 분류
- Classification
- OpenAI
- Machine Learning
- 티스토리챌린지
- GPT-4
- supervised learning
- gpt
- LG
- regression
- 회귀
- 지도학습
Archives
- Today
- Total
SYDev
[Data Structure] Chapter 12: 균형 잡힌 이진 탐색 트리 - AVL 트리 본문
Data Structure & Algorithm/Data Structure
[Data Structure] Chapter 12: 균형 잡힌 이진 탐색 트리 - AVL 트리
시데브 2023. 9. 13. 17:49이진 탐색 트리의 단점을 개선한 자료 구조 중 하나인 AVL 트리를 이해하고, 구현해보자.
이진 탐색 트리의 문제점
이진 탐색 트리는 다음 그림과 같이 균형이 맞지 않을수록 $O(n)$에 가까운 시간 복잡도를 보인다.

이렇듯 저장 순서에 따라 탐색의 성능에 큰 차이를 보이는 것이 이진 탐색 트리의 단점이다.
AVL 트리의 이해
- 이진 탐색 트리가 자동으로 균형을 잡을 수 있도록 개선한 트리 중 하나가 AVL 트리이다.
- G. M. Adelson-Velskii와 E. M. Landis에 의해 고안되었으며, 그들의 이름을 따서 정해졌다.
- AVL 트리에서는 균형의 정도를 표현하기 위해 '균형 인수(Balance Factor)'라는 것을 사용한다.
- 리밸런싱(rebalancing): 균형을 잡기 위한 트리 구조의 재조정을 의미한다.
- 리밸런싱은 균형 인수의 절댓값이 2 이상인 경우에 진행된다.
균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이

리밸런싱이 필요한 상태
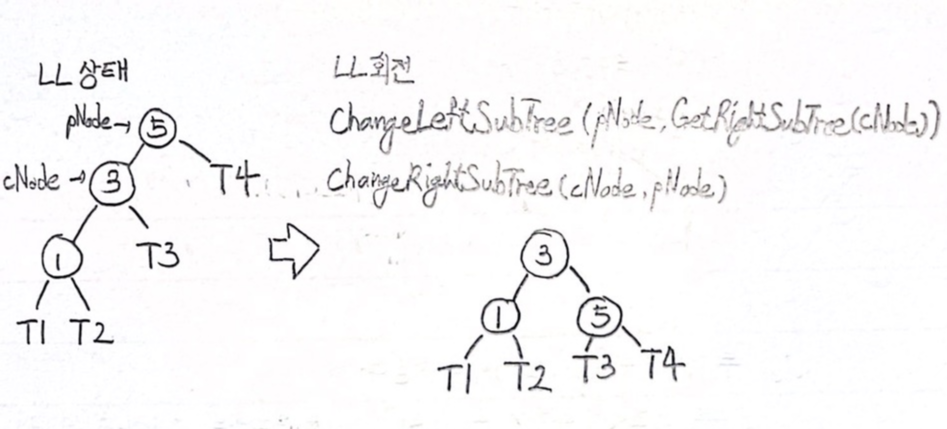
리밸런싱이 필요한 상태로는 LL상태, RR상태, LR상태, RL상태의 4가지로 정리된다.
LL상태
RR상태

LR상태

RL상태

AVL 트리의 구현
- AVL 트리를 구현하기 위해서 이전에 구현한 이진 탐색 트리를 이용한다.
- 리밸런싱을 진행하는데 필요한 도구들을 포함한 파일을 추가한다.
- 이전에 구현한 BinarySearchTree2의 insert와 remove 함수에 리밸런싱 과정만 추가한다.
파일명: AVLRebalance.h
#ifndef __AVL_REBALANCE_H__
#define __AVL_REBALANCE_H__
#include "BinaryTree3.h"
BTreeNode * Rebalance(BTreeNode ** pRoot);
#endif
파일명: AVLRebalance.c
#include <stdio.h>
#include "AVLRebalance.h"
int GetHeight(BTreeNode * bst) //트리의 높이 계산
{
int leftH;
int rightH;
if(bst == NULL)
return 0;
leftH = GetHeight(GetLeftSubTree(bst));
rightH = GetHeight(GetRightSubTree(bst));
if(leftH > rightH)
return leftH + 1;
else
return rightH + 1;
}
int GetHeightDiff(BTreeNode * bst) //두 서브 트리의 '높이의 차(균형 인수)'를 반환
{
int lsh; //left sub tree height
int rsh; //right sub tree height
if(bst == NULL)
return 0;
lsh = GetHeight(GetLeftSubTree(bst));
rsh = GetHeight(GetRightSubTree(bst));
return lsh - rsh;
}
BTreeNode * RotateLL(BTreeNode * bst)
{
BTreeNode * pNode;
BTreeNode * cNode;
pNode = bst;
cNode = GetLeftSubTree(pNode);
ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
ChangeRightSubTree(cNode, pNode);
return cNode;
}
BTreeNode * RotateRR(BTreeNode * bst)
{
BTreeNode * pNode;
BTreeNode * cNode;
pNode = bst;
cNode = GetRightSubTree(pNode);
ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
ChangeLeftSubTree(cNode, pNode);
return cNode;
}
BTreeNode * RotateLR(BTreeNode * bst)
{
BTreeNode * pNode;
BTreeNode * cNode;
pNode = bst;
cNode = GetLeftSubTree(pNode);
ChangeLeftSubTree(pNode, RotateRR(cNode)); //부분적 RR회전
return RotateLL(pNode);
}
BTreeNode * RotateRL(BTreeNode * bst)
{
BTreeNode * pNode;
BTreeNode * cNode;
pNode = bst;
cNode = GetRightSubTree(pNode);
ChangeRightSubTree(pNode, RotateLL(cNode)); //부분적 LL회전
return RotateRR(pNode);
}
BTreeNode * Rebalance(BTreeNode ** pRoot)
{
int hDiff = GetHeightDiff(*pRoot);
//균형 인수가 +2 이상이면 LL상태 or LR상태
if(hDiff > 1)
{
if(GetHeightDiff(GetLeftSubTree(*pRoot)) > 0)
*pRoot = RotateLL(*pRoot);
else
*pRoot = RotateLR(*pRoot);
}
if(hDiff < -1)
{
if(GetHeightDiff(GetRightSubTree(*pRoot)) < 0)
*pRoot = RotateRR(*pRoot);
else
*pRoot = RotateRL(*pRoot);
}
return *pRoot;
}
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
. . . .
*pRoot = Rebalance(pRoot);
}
BTreeNode * BSTRemove(BTreeNode ** pRoot, BSTData target)
{
. . . .
*pRoot = Rebalance(pRoot);
return dNode;
}
파일명: AVLTreeMain.c
#include <stdio.h>
#include <stdlib.h>
#include "BinarySearchTree3.h"
int main(void)
{
BTreeNode * AVLRoot;
BTreeNode * clNode; //current left node
BTreeNode * crNode; //current right node
BSTMakeAndInit(&AVLRoot);
BSTInsert(&AVLRoot, 1);
BSTInsert(&AVLRoot, 2);
BSTInsert(&AVLRoot, 3);
BSTInsert(&AVLRoot, 4);
BSTInsert(&AVLRoot, 5);
BSTInsert(&AVLRoot, 6);
BSTInsert(&AVLRoot, 7);
BSTInsert(&AVLRoot, 8);
BSTInsert(&AVLRoot, 9);
printf("루트 노드: %d \n", GetData(AVLRoot));
clNode = GetLeftSubTree(AVLRoot);
crNode = GetRightSubTree(AVLRoot);
printf("왼쪽1: %d, 오른쪽1: %d \n", GetData(clNode), GetData(crNode));
clNode = GetLeftSubTree(clNode);
crNode = GetRightSubTree(crNode);
printf("왼쪽2: %d, 오른쪽2: %d \n", GetData(clNode), GetData(crNode));
clNode = GetLeftSubTree(clNode);
crNode = GetRightSubTree(crNode);
printf("왼쪽3: %d, 오른쪽3: %d \n", GetData(clNode), GetData(crNode));
clNode = GetLeftSubTree(clNode);
crNode = GetRightSubTree(crNode);
printf("왼쪽4: %d, 오른쪽4: %d \n", GetData(clNode), GetData(crNode));
return 0;
}루트 노드: 5
왼쪽1: 4, 오른쪽1: 6
왼쪽2: 3, 오른쪽2: 7
왼쪽3: 2, 오른쪽3: 8
왼쪽4: 1, 오른쪽4: 9
- 윤성우, <윤성우의 열혈 자료구조>, 오렌지미디어, 2022.04.11
728x90
반응형
'Data Structure & Algorithm > Data Structure' 카테고리의 다른 글
| [Data Structure] Chapter 13-2: 충돌(Collision) 문제의 해결책 (0) | 2023.09.18 |
|---|---|
| [Data Structure] Chapter 13-1: 빠른 탐색을 보이는 해쉬 테이블 (1) | 2023.09.17 |
| [Data Structure] Chapter 11-2: 이진 탐색 트리 (0) | 2023.09.12 |
| [Data Structure] Chapter 11-1: 탐색의 이해와 보간 탐색 (1) | 2023.09.11 |
| [Data Structure] Chapter 10-2: 복잡하지만 효율적인 정렬 알고리즘 (0) | 2023.09.11 |




